Extremwertaufgaben mit Nebenbedingung
Inhalt dieser Webseite
Was ist eine Extremwertaufgabe?
Einheitliche Darstellung
Notwendige und hinreichende Bedingungen
Figuren mit größtem Flächeninhalt
Figuren mit kleinstem Flächeninhalt
Figuren mit kleinstem Umfang		 Körper mit größtem Volumen
Körper mit kleinster Oberfläche
Paare von Aufgaben
Extremwertaufgaben im Internet
Referenzen
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist eine Extremwertaufgabe mit Nebenbedingung?
In einer Extremwertaufgabe oder (im Schülerjargon) Minimax-Aufgabe wird gefragt, an welcher Stelle eine Funktion einen Maximal- oder Minimalwert annimmt.  Das Besondere dieser Aufgaben ist, dass die Funktion zunächst nur durch zwei Variable ausgedrückt werden kann. Zwischen den Variablen existiert aber eine Gleichung, die es gestattet, eine Variable durch die andere zu ersetzen und die Funktion so in eine Funktion mit einer Variablen umzuformen. 

Es folgt ein einfaches Beispiel.
...... Welche Maße hat ein Rechteck, dessen Flächeninhalt maximal bei konstantem Umfang ist? 
Sind x und y die Seitenlängen und u der konstante Umfang, so ist der Flächeninhalt A=xy und die Gleichung zwischen den Variablen u=2x+2y oder y=u/2-x. 
Das führt zur "Zielfunktion" mit A(x)=xy=x(u/2-x)=(u/2)x-x². 
...... Der Graph von A(x) = -x²+(u/2)x ist eine nach unten geöffnete Parabel, die in x = u/4 eine Hochstelle hat. 
Mit x = u/4 ist auch y = u/4. 

Ergebnis: Das gesuchte Rechteck ist ein Quadrat.
Auf dieser Seite habe ich Extremwertaufgaben zusammengestellt, die auf meiner Homepage an unterschiedlichen Stellen vorkommen. Es hat sich so ergeben, dass sie sich nur auf Figuren oder Körper beziehen. Darunter sind etliche Klassiker.

Einheitliche Darstellung     top
Da Extremwertaufgaben nach einem gleichen Muster gelöst werden können, werden sie im Folgenden in gleicher Weise dargestellt. 
Die einführende Aufgabe und ihre Lösung sehen dann wie folgt aus.
01) Welche Maße hat ein Rechteck, dessen Flächeninhalt maximal bei konstantem Umfang ist? 
...... Nebenbedingung: Der Umfang des Rechtecks ist u = 2x+2y. Dann ist y = u/2-x.

Zielfunktion: A = xy oder A(x) = x(u/2-x) oder A(x) = (1/2)ux-x².

WeitereRechnung
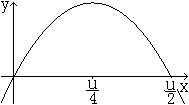
A'(x) = (1/2)u-2x. A'(x) = 0 führt zu (1/2)u-2x = 0 oder x = u/4. 
A''(x) = -2 ist negativ und so ist x eine Maximalstelle. 

Lösung: x = y = u/4. 
Das Rechteck ist ein Quadrat. 
Anmerkungen
Für die Lösung stehen die beiden folgenden Sätze aus der Differentialrechnung bereit.
Satz 1: 
Wenn f(x) eine stetige und 2x differenzierbare Funktion ist und an der Stelle x die Aussagen f '(x)=0 und f ''(x)<0 gelten, so ist x eine (lokale) Hochstelle.
Satz 2: 
Wenn f(x) eine stetige und 2x differenzierbare Funktion ist und an der Stelle x die Aussagen f '(x)=0 und f ''(x)>0 gelten, so ist x eine (lokale) Tiefstelle.

Zur Festlegung der Extremwerte reicht die erste Ableitung. Mit der zweiten Ableitung stellt man sicher, ob der "Kandidat" auch wirklich ein Extremwert ist. Das geht oft schon aus dem Zusammenhang hervor, ist aber mathematisch gesehen nicht stichhaltig. -
Im Allgemeinen haben die Aufgaben nur eine Lösung und die lokalen Extremwerte sind auch die gesuchten. Streng genommen müsste man alle Extremstellen, auch Randstellen, in Betracht ziehen. 

Notwendige und hinreichende Bedingungen      top
Gerne verwendet man im Zusammenhang mit den beiden Sätzen Satz 1 und Satz 2 von oben die fundamentalen Begriffe notwendig und hinreichend. (Ich beschränke mich in den folgenden Überlegungen auf Tiefstellen.)
Ich fand dazu im Internet mehrfach die folgenden Aussagen zur Bestimmung einer Tiefstelle. 
Notwendige Bedingung: f'(x)=0
Hinreichende Bedingung: f''(x)>0
Sie sind missverständlich, um nicht zu schreiben falsch.
Es muss heißen: 
Notwendige Bedingung: f'(x)=0
Hinreichende Bedingung:  f'(x)=0 und f''(x)>0

Die Erste-Ableitung-Prüfung f'(x)=0 ist für differenzierbare Funktionen für lokale Tiefstellen immer erfüllt. 
Die Bedingung f'(x)=0 ist also eine notwendige Bedingung.
Die Zweite-Ableitung-Prüfung f''(x)>0 ist für sich genommen keine hinreichende Bedingung für die Existenz einer Tiefstelle. Es muss noch die Erste-Ableitung-Prüfung dazukommen.
Es stellt sich noch die Frage, wie man verfährt, wenn der Satz versagt. 
Zum Beispiel liegt bei der Funktion mit f(x)=x4 in x=0 eine Tiefstelle vor, es gilt aber neben f'(0)=0 auch f''(0)=0. Satz 1 versagt.
Das Beispiel beweist, dass die Bedingung [f'(x)=0 und f''(x)>0] nur hinreichend ist.

Ein zweites Beispiel ist die Funktion mit f(x)=|x|. Sie hat in x=0 eine Tiefstelle, ist aber an dieser Stelle nicht differenzierbar. 

In beiden Fällen gilt die zweite Bedingung  f''(x)>0 nicht. Man muss sich da etwas anderes überlegen, um die Tiefstelle nachzuweisen.

Figuren mit größtem Flächeninhalt     top
02) Welches Rechteck im gleichschenkligen Dreieck hat den größten Flächeninhalt?
...... Nebenbedingung: Nach dem zweiten Strahlensatz ist x:c=(h-y):h oder xh=c(h-y) oder y=h-(h/c)x.

Zielfunktion: A=xy oder A(x)=x[h-(h/c)x]=hx-(h/c)x²

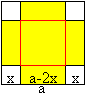
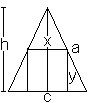
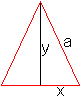
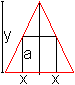
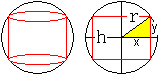
Lösung: x=c/2, y=h/2
Das Rechteck wird bestimmt durch die Mittelparallele bezüglich der Grundseite.
03) Welches Dreieck kopfüber im gleichschenkligen Dreieck hat den größten Flächeninhalt?
......
 Nebenbedingung: Nach dem zweiten Strahlensatz ist x:c=(h-y):h oder xh=c(h-y) oder y=h-(h/c)x.

Zielfunktion: A=(1/2)xy oder 2A(x)=x[h-(h/c)x]=hx-(h/c)x²

Weitere Rechnung wie Aufgabe 02
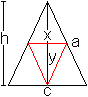
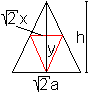
Lösung: x=a/2, y=h/2
Das gesuchte Dreieck ist das Mittendreieck.
Anmerkung
Ein konstanter Faktor wie 1/2 in A=(1/2)xy muss nicht in der Rechnung mitgeschleppt werden. 
Die Lage des Extremwertes ändert sich nicht, wenn man ihn der Fläche zuschlägt.
04) Welches Dreieck kopfüber im Halbkreis hat den größten Flächeninhalt?
...... Nebenbedingung: Nach dem Satz des Pythagoras gilt x²+y²=r² oder y²=r²-x²
Zielfunktion: A=xy oder A²=x²y²  oder A2= x2(r2-x2)=r2x2-x4
Weitere Rechnung
Die Bedingung (A²)'=0 ergibt 2r²x-4x³=0 oder 2r²=4x² oder x²=(1/2)r². 
Die nur zutreffende positive Lösung ist x=(1/2)sqrt(2)r und daraus ergibt sich y=(1/2)sqrt(2)r.
Zu ergänzen ist noch, dass für die 2.Ableitung an der Stelle x=(1/2)sqrt(2)r gilt: (A²)''=2r²-12x²=2r²-6r²<0.
Lösung: x=y=(1/2)sqrt(2)r 
Das größte Dreieck ist gleichschenklig-rechtwinklig.
Anmerkung
Man vermeidet einen Wurzelterm in Aufgabe 04, weil man nicht f, sondern q=f² betrachtet.
Der folgende Satz rechtfertigt dieses Vorgehen.
Satz: 
Wenn die Quadrat-Funktion mit q(x)=f ²(x) eine differenzierbare Funktion ist 
und an der Stelle x die Aussagen f(x)>0, q'(x)=0 und q''(x)<0 gelten, so ist x eine Hochstelle.
Beweis: 
Es ist zu zeigen, dass die Aussagen f '(x)=0 und f ''(x)<0 gelten.
Es gilt nach der Kettenregel q'(x)=2f(x)f '(x). Daraus folgt f '(x)=0 wegen f(x)>0.
Es gilt nach der Produktregel q''(x)=2[f '(x)]²+2f(x)f ''(x)=2f(x)f ''(x). Daraus folgt f ''(x)<0 wegen f(x)>0, wzbw..

Streng genommen müsste man bei Anwendung dieses Satzes beweisen, dass A(x)>0 gilt. 

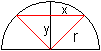
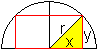
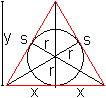
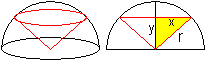
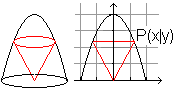
05) Welches Rechteck im Halbkreis hat den größten Flächeninhalt?
...... Nebenbedingung: x²+y²=r² oder y²=r²-x²
Zielfunktion: A=2xy oder (1/4)A²=x²y² oder (1/4)A²=x²(r²-x²)
Weitere Rechnung wie Aufgabe 04
Lösung: x=y=(1/2)sqrt(2)r 
Das größte Rechteck ist ein Doppelquadrat.
06) Welches gleichschenklige Trapez im Halbkreis hat den größten Flächeninhalt?
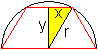
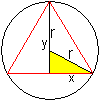
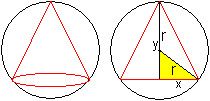
...... Nebenbedingung:  Nach dem Satz des Pythagoras gilt  x²+y²=r² oder y²=r²-x².
Zielfunktion: A=[(2x+2r)/2]y=(x+r)y oder A=(x+r)(r²-x²) oder A2= -x4-2rx3+2r3x+r4
Lösung: x=r/2 und y=(1/2)sqrt(3)r 
Das Trapez ist ein halbes regelmäßiges Sechseck.
07) Welches gleichschenklige Dreieck im Kreis hat den größten Flächeninhalt?
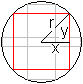
...... Nebenbedingung:  Nach dem Satz des Pythagoras gilt r²=(y-r)²+x² oder x²=r²-(y-r)².

Zielfunktion:  A=xy oder A²=x²y² oder  A²=y²[r²-(y-r)²] oder A²= -y4+2ry3

Lösung: y=(3/2)r und x=(1/2)sqrt(3)r. 
Das Dreieck ist gleichseitig.
08) Welches Rechteck im Kreis hat den größten Flächeninhalt?
...... Nebenbedingung: Nach dem Satz des Pythagoras gilt  x²+y²=r² oder y²=r²-x².

Zielfunktion: (1/4)A=xy oder A²/16=x²(r²-x²)
Weitere Rechnung wie Aufgabe 04.
Lösung: x=y=(1/2)sqrt(2)r. 
Das Rechteck ist ein Quadrat der Seitenlänge sqrt(2)r.
Anmerkung
Das Ergebnis passt zu Aufgabe 05, bei der ein Halbkreis betrachtet wird.
09) Welches gleichschenklige Dreieck im Parabelsegment hat den größten Flächeninhalt?
...... Nebenbedingung: Die Parabel soll der Gleichung y=4-x² genügen.

Zielfunktion: A=xy oder A(x)=(4-x²)x oder A=4x-x³

Lösung: x=(2/3)sqrt(3) und y=8/3
10) Welches Rechteck im Parabelsegment hat den größten Flächeninhalt?
...... Nebenbedingung:  y=4-x² 

Zielfunktion: A=2xy oder (1/2)A(x)=x(4-x²)

Lösung: Das Rechteck hat die Seiten 2x=(2/3)sqrt(3) LE und y=8/3 LE.
LE steht für Längeneinheiten.
11) Welches gleichschenklige Trapez  im Parabelsegment hat den größten Flächeninhalt?
......
 Nebenbedingung: Die Parabel soll der Gleichung y=-x²+1 genügen.

Zielfunktion: A=(1/2)(2+2x)y oder A(x)=(x+1)(-x²+1) oder A(x)==-x³+x-x²+1


Lösung: Das maximale Trapez hat die Grundseiten 2 LE, 2/3 LE und die Höhe 8/9 LE.
12) Für welchen Parameter a ist der Flächeninhalt des gekennzeichneten Parabelsegments mit y=ax² maximal?
...... Schnittpunkt der beiden Parabeln:
Ansatz: ax²=-x²+1
Dann ist (a+1)x²=1 oder x²=1/(a+1) und xs=sqrt[1/(a+1)]=(a+1)-1/2
Weiter ist ys=-1/(a+1)+1=a/(a+1) 
Weitere Rechnung
Für die Fläche (1/2)A(a) gilt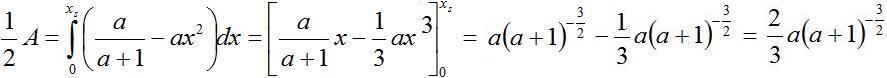
...
Dann ist nach der Produktregel die Ableitung (3/4)A'(a) wie folgt.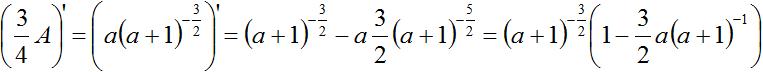
...
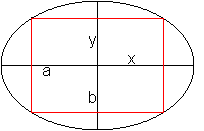
[(3/4)A]'=0 führt zu 1-(3/2)a/(a+1)=0 oder 2(a+1)=3a oder a=2.
Lösung: Die Fläche ist maximal für a=2.
13) Welches Rechteck in der Ellipse hat den größten Flächeninhalt?
...... Nebenbedingung: x²/a²+y²/b²=1 oder y²=b²-(b²/a²)x²

Zielfunktion: A=4xy oder A²=16x²y²=16x²[b²-(b²/a²)x²]=16b2x2-(16b2/a2)x4

Weitere Rechnung
(A²)'=32b²x-(64b²/a²)x³=32b²x(1-2x²/a²)
(A²)'=0  führt zu 1-2x²/a²=0  oder x²=(1/2)a² oder x=(1/2)sqrt(2)a oder 2x=sqrt(2)a. 
Die Gleichung  y²=b²-(b²/a²)x² führt zu y=(1/2)sqrt(2)b odr 2y=sqrt(2)b.
Die zweite Ableitung (A²)''=-4x/a²<0 stellt sicher, dass das Rechteck wirklich maximal ist.
Lösung: Das Rechteck hat die Seiten 2x=sqrt(2)a und 2y=sqrt(2)b.
Die Seiten des Rechtecks stehen im Verhältnis a:b.
Anmerkung
Artet die Ellipse zu einem Kreis aus, gilt also a=b=r, so ist 2x=2y=sqrt(2)r und aus dem maximalen Rechteck wird ein Quadrat wie in Aufgabe 08.
14) Welches gleichschenklige Dreieck hat bei konstantem Umfang den größten Flächeninhalt?
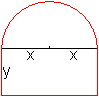
...... Nebenbedingung: U=2x+2a, a²=x²+y² und y²=(U/2)²-Ux

Zielfunktion: A=xy oder A²=x²y²=x²[(U/2)²-Ux]=(1/4)U²x²-Ux³

Lösung: Das Dreieck hat die Grundseite 2x=U/3 und die Schenkel a=U/3. 
Das gesuchte Dreieck ist gleichseitig.
15) Welche Form muss eine Figur aus einem Rechteck mit aufgesetztem Halbkreis haben, damit bei konstantem Umfang der Flächeninhalt maximal wird? (Fensteraufgabe)
...... Nebenbedingung: U=2x+2y+Pi*x

Zielfunktion: A=Ux-2x²-(Pi/2)x²

Lösung: x=y=U/(4+Pi)
Das Rechteck ist ein Doppelquadrat.
16) Bei welchem Winkel hat ein gleichschenkliges Trapez aus drei bekannten Seiten den größten Flächeninhalt?
(Eine Rinne soll möglichst viel Wasser fassen.)
... Statt A=A(alpha) wird A=A(x) untersucht.
Nebenbedingung: s²=b²-x² oder s=sqrt(b²-x²). 
Zielfunktion: A(x)=(1/2)(b+b+2s)x oder A(x)=[-2x²+b²+b*sqrt(b²-x²)]/sqrt(b²-x²)
Weitere Rechnung
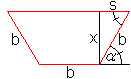
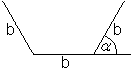
A'(x)=b+(-2x²)/[2sqrt(b²-x²)]+sqrt(b²-x²)=[-2x²+b²+b*sqrt(b²-x²)]/sqrt(b²-x²)
A'(x)=0 bedeutet -2x²+b²+b*sqrt(b²-x²)=0 oder b*sqrt(b²-x)=2x²-b² oder b²(b²-x²)=(2x²-b²)² 
oder b4-b²x²=4x4-4b²x²+b4 oder -b²x²=4x4-4b²x² oder 4x4 =3b²x². 
Das führt zu x=0 und x²=(3/4)b² bzw. x=(1/2)sqrt(3)b und x=-(1/2)sqrt(3)b. 
Für das Problem ist die Lösung x=(1/2)sqrt(3)b zutreffend. Das führt zu sin(alpha)=(1/2)sqrt(3) oder alpha=60°.
Auf die zweite Ableitung verzichte ich.
Es stellt sich die Frage, weshalb das Trapez auf den Kopf gestellt wird.
......  Das liegt daran, dass die Aufgabe meist so formuliert wird.
Eine Rinne wird aus drei Brettern gleicher Breite gebildet, einem Bodenbrett und zwei Seitenbrettern. 
Wie groß muss der Neigungswinkel der Seitenbretter sein, wenn durch die Rinne möglichst viel Wasser fließen soll?
Für alpha=60° ist das Trapez übrigens ein halbes regelmäßiges Sechseck.
17) Welche Maße muss ein Fußballplatz haben, damit ihn eine Laufbahn von a=400 m umschließt und er möglichst groß ist? (Sportplatzaufgabe)
... Nebenbedingung:  a=2y+2pi*x oder y=(1/2)a-pi*x
Zielfunktion: A=2xy oder A(x)=2x[(1/2)a-pi*x]=ax-2pi*x²
Lösung: Der Fußballplatz hat die Maße y=100m und 2x=63,7m.
18) Einem Schäfer stehen Zaunelemente der Gesamtlänge g zur Verfügung. Damit will er eine rechteckige Einzäunung bauen, wobei eine Seite von einer Felswand gebildet wird. Welche Form muss er dem Rechteck geben, damit die Fläche möglichst groß wird?
...... Nebenbedingung: s=2y+x oder x=s-2y 
Zielfunktion: A=xy oder A(y)=y(s-2y)=-2y²+sy 

Lösung: y=(1/4)s und  x=(1/2)s
Das Rechteck ist ein Doppelquadrat.

Figuren mit kleinstem Flächeninhalt       top
19) Welches Dreieck um ein Quadrat hat den kleinsten Flächeninhalt? 
...... Nebenbedingung: Nach dem zweiten Strahlensatz gilt a:y=(x-a/2):x oder y=2ax/(2x-a).

Zielfunktion:  A=xy oder A(x)=2ax²/(2x-a)

Lösung: x=2a und y=2a
Die Grundseite und die Höhe des Dreiecks sind gleich lang.
20) Welches Dreieck um einen Kreis hat den kleinsten Flächeninhalt? 
...... Nebenbedingung: s²r²=x²y²-2rx²y+x²r² oder x²=r²y/(y-2r)

Zielfunktion: A²=x²y² oder A²=r²y³/(y-2r)

Lösung: Das Dreieck hat die Grundseite x=sqrt(3)r und die Höhe y=3r.
Das Dreieck ist gleichseitig mit der Seitenlänge 2sqrt(3)r.
21) Welches Dreieck um einen Halbkreis hat den kleinsten Flächeninhalt?
...... Nebenbedingung: x²y²=r²x²+r²y²

Zielfunktion: A²=x²y²= r2x4/(x2-r2)

Weitere Rechnung
(A²)'=[4r2x3(x2-r2)-2x(r2x4)]/(x2-r2)2. 
Der Zähler wird Null gesetzt und weiter verfolgt: 
4r2x3(x2-r2)-2x(r2x4)=0 oder 4r2x5-4r4x3-2r2x5=2r2x3(x2-2r2)=0.
Eine brauchbare Lösung erhält man in x²-2r²=0 oder x=sqrt(2)r. Dann ist auch y=sqrt(2)r.
Lösung: Das Dreieck hat die Grundseite 2x=2sqrt(2)r und die Höhe y=sqrt(2)r. 
Das größte Dreieck ist gleichschenklig-rechtwinklig. 
Spiegelt man das Dreieck an der Hypotenuse, entsteht ein Quadrat, aus dem Halbkreis wird der Inkreis. 

Figuren mit kleinstem Umfang       top
22) Welches Rechteck hat bei konstantem Flächeninhalt den kleinsten Umfang? 
...... Nebenbedingung: A=xy oder y=A/x

Zielfunktion:  (1/2)U=x+y oder (1/2)U=x+A/x oder (1/2)U=x+Ax-1

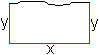
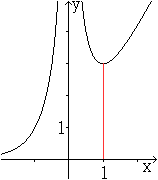
Lösung: x=y=sqrt(A). 
Das Rechteck ist ein Quadrat.
23) Welches gleichschenklige Dreieck hat bei konstantem Flächeninhalt den kleinsten Umfang? 
...... Nebenbedingung: A=xy oder y=A/x 

Zielfunktion: (1/2)U=x+a=x+sqrt(x²+y²) oder (1/2)U(x)=x+sqrt(x²+A²/x²)

Oben wurde gezeigt, dass das Dreieck mit dem kleinsten Flächeninhalt bei konstantem Umfang das gleichseitige Dreieck ist. Es ist anzunehmen, dass auch hier das gleichseitige Dreieck das gesuchte ist. 
Das bestätigt der folgende Graph.
...... Statt einer umfänglichen Rechnung wird hier die Funktion mit (1/2)U(x)=x+sqrt(x²+A²/x²) gezeichnet.

Bei einem gleichseitigen Dreieck ist A=(1/4)sqrt(3)(2x)². Dann ist A=sqrt(3)x² oder A²=3x4.

Setzt man A²=3 in die Funktionsgleichung ein, ergibt sich (1/2)U(x)=x+sqrt(x²+3/x²).

Der Graph hat eine Minimalstelle für x=1, da A²=3 gewählt wird.
Lösung: Das Dreieck ist gleichseitig.

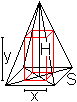
Körper mit größtem Volumen       top
24) Welcher Zylinder im Kegel hat das größte Volumen?
......
 Nebenbedingung: (h-y):h=x:r (2.Strahlensatz) oder y=h-(h/r)x

Zielfunktion: V=pi*x²y oder V(x)=pi*hx²-(pi*h/r)x³

Lösung: x=(2/3)r und y=(1/3)h
25) Welcher Zylinder in der Kugel hat das größte Volumen?
...... Nebenbedingung: : x²+y²=r² (Satz des Pythagoras) oder x²=r²-y²

Zielfunktion: V=pi*x²y oder V(y)=pi*r²y-pi*y³

Lösung: y=(1/3)sqrt(3)r und x=(1/3)sqrt(6)r
26) Welcher Kegel kopfüber im Kegel hat das größte Volumen? 
...... Nebenbedingung: (h-y):h=x:r (2.Strahlensatz) oder y=h-(hx)/r

Zielfunktion: V=(1/3)pi*x²y oder 3V(x)=pi*hx²-(pi*h/r)x³
 
Weitere Rechnung wie Aufgabe 24
Lösung: x=(2/3)r und y=(1/3)h
27) Welcher Kegel in der Kugel hat das größte Volumen?
...... Nebenbedingung: x²=r²-(y-r)² (Satz des Pythagoras) oder x²=2ry-y²

Zielfunktion: V=(1/3)pi*x²y oder V(y)=(pi/3)(2ry²-y³) oder V(y)=(2/3)pi*ry²-(1/3)pi*y³
 
Lösung: y=(4/3)r und x=(2/3)sqrt(2)r und y:x=sqrt(2):1 
28) Welcher Kegel in der Halbkugel hat das größte Volumen?
...... Nebenbedingung: r²=x²+y² (Satz des Pythagoras) oder x²=r²-y²
Zielfunktion: 
V=(1/3)pi*x²y oder V(y)=(1/3)pi*(r²-y²)y oder V(y)=(1/3)pi*r²y-(1/3)pi*y³
Lösung: y=(1/3)(sqrt(3)r und x=(1/3)sqrt(6)r  und y:x=1:sqrt(2)
29) Welcher Kegel im Paraboloid hat das größte Volumen?
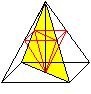
...... Nebenbedingung:  y=4-x² (Funktionsgleichung)

Zielfunktion: V=(1/3)pi*x²y oder V(x)=(pi/3)x²(4-x²) oder V(x)=(4/3)pi*x2-(1/3)pi*x4

Lösung: x=sqrt(2) und y=2 und  y:x=sqrt(2):1
30) Welche Pyramide in der Kugel hat das größte Volumen?
... Nebenbedingung: 
R²=[1/2)sqrt(2)]²x²+(y-R)² oder (1/2)x²+y²=2yR oder x²=4yR-2y²

Zielfunktion: V(y)=(1/3)x²y=(1/3)(4Ry-2y²)y oder V(y)=(4/3)Ry²-(2/3)y³

Lösung: y=(4/3)R und x=(4/3)R
31) Welches Prisma in einer quadratischen Pyramide hat das größte Volumen?
......... Nebenbedingung: 
Nach dem 2.Strahlensatz gilt [sqrt(2)S/2] : [sqrt(2)x/2]=H:(H-y) oder y=H-(H/S)x.

Zielfunktion:   V=x²y oder V(x)=x²[H-(H/S)x]=Hx²-(H/S)x³

Lösung: x=(2/3)S und y=(1/3)H
32) Welche Pyramide, die in einer quadratischen Pyramide kopfüber liegt, hat das größte Volumen?
...... ... Nebenbedingung:
Nach dem 2.Strahlensatz gilt die Proportion h:(h-y)=(a/2):(x/2) oder y=(ah-hx)/a. 

Zielfunktion: V=(1/3)x²y oder V(x)=(1/3)hx²-(1/3)(h/a)x³
 
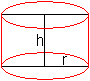
Lösung: x=(2/3)a  und y=(1/3)a
33) Welcher Zylinder hat bei konstanter Oberfläche das größte Volumen?
 
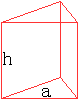
...... Nebenbedingung: O=2pi*r(r+h) oder h=(O-2pi*r²)/(2pi*r)

Zielfunktion: V=pi*r²h oder V(r)=Or/2-pi*r³

Lösung: r=sqrt[O/(6pi)] und h=sqrt[2O/(6pi)]
Die Höhe und der Durchmesser des Zylinders sind gleich.
34) Welcher oben offene Zylinder hat bei konstanter Oberfläche das größte Volumen?
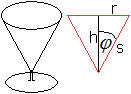
...... Nebenbedingung: O=pi*r²+2pi*rh oder h=(O-pi*r²)/(2pi*r)

Zielfunktion: V=pi*r²h oder V(r)=Or-pi*r³

Lösung: r=sqrt[O/(3pi)] und h=sqrt[O/(3pi)]
Der Durchmesser ist doppelt so groß wie die Höhe. 
35) Welcher Kegel hat bei konstanter Seitenlinie das größte Volumen?
...... Nebenbedingung: h=s*cos(phi) und r=s*sin(phi)
s ist die konstante Seitenlinie.

Zielfunktion: V=(1/3)pi*r²h.
V(phi)=(1/3)pi*s³[sin²(phi)cos(phi)]=(1/3)pi*s³[cos(phi)-cos³(phi)]

Weitere Rechnung
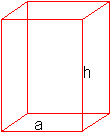
V'(phi)=(1/3)pi*s³[-sin(phi)+3cos²(phi)sin(phi)]. 
V'(phi)=0 führt zu cos(phi)=(1/3)sqrt(3) oder phi=54,74°.
Lösung: 
Ein kegelförmiges Glas fasst bei konstanter Seitenlinie dann die größte Menge, wenn der Öffnungswinkel angenähert 109,5° beträgt.
36) Welches quadratische Prisma hat bei konstanter Oberfläche das größte Volumen?
...... Nebenbedingung: O=2a²+4ah oder h=(O-2a²)/(4a) 

Zielfunktion:  V=a²h oder V(a)=a²(O-2a²)/(4a)=Oa/4-a³/2 

Lösung:  a=sqrt(O/6)=(1/6)sqrt(6O), h=(1/6)sqrt(6O) 
Das Prisma ist ein Würfel.
37) Welches regelmäßige, dreiseitige Prisma hat bei konstanter Oberfläche das größte Volumen?
...... Nebenbedingung: O=(1/2)sqrt(3)a²+3ah oder h=O/(3a)-(1/6)sqrt(3)a

Zielfunktion:  V=(sqrt(3)/12)Oa-(sqrt(3)/8)a³ 

Rechnung 
Ergebnis:

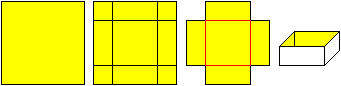
38) Wie müssen quadratische Eckstücke, die man von einem gegeben Quadrat abschneidet, bemessen sein, damit eine Schachtel mit größtem Volumen entstehen kann?
......
......
 Zielfunktion: V(x)=(a-2x)²x=4x³-4ax²+a²x
Weitere Rechnung
V'(x)=12x²-8ax+a², V''(x)=24x-8a. 
V'(x)=0 ergibt 12x²-8ax+a²=0 oder x²-2ax/3+a²/12=0. 
Diese quadratische Gleichung hat die Lösungen  x1=a/6 und x2=a/2.
Für x2=a/2 gibt es keine Schachtel. Die Lösung ist x1=a/6 oder (a-2 x1)=2a/3. 
Mit V''(a/6)= - 4a<0 ist sichergestellt, dass ein Maximum vorliegt.
Lösung: x= a/6

Körper mit kleinster Oberfläche       top
39) Welches quadratische Prisma hat bei konstantem Volumen die kleinste Oberfläche?
...... Nebenbedingung: V=a²h oder h=V/a²

Zielfunktion: O=2a²+4ah=O=2a²+4V/a

Lösung: a=h=V1/3
Das Prisma ist ein Würfel.
40) Welcher Zylinder hat bei konstantem Volumen die kleinste Oberfläche?
...... Nebenbedingung: V=pi*r²h oder h=V/(pi*r²)

Zielfunktion: O=2pi*r(r+h) oder O(r)=2pi*r²+2V/r

Lösung: r=[V/(2pi)]1/3, h=[4V/pi]1/3 
Die Höhe und der Durchmesser des Zylinders sind gleich.

Paare von Aufgaben       top
Auf dieser Seite werden zwei Aufgaben behandelt, die ich auch in einem Lehrbuch von 1938 fand.
......
Es sind Aufgabe 33 und Aufgabe 40, in denen einmal nach dem maximalen Volumen, einmal nach der maximalen Oberfläche gefragt wird. In beiden Fällen haben die gesuchten Zylinder die gleiche Form, nämlich  (2r)/h=1. Vom Gefühl her ist das nicht erstaunlich, dass mit einem maximalen Volumen eine minimale Oberfläche einhergeht. 
Aber gibt es eine rechnerische Begründung? 

Es folgt dazu eine Überlegung (nach Torsten Sillke).
Man führt das Verhältnis x=2r/h ein. Dann gilt h=2r/x.
Das bedeutet V=pi*r²h=pi*r²*(2r/x)=2*pi*r³/x und O=2*pi*r(r+h)=2*pi*r(r+2r/x)=2*pi*r²(1+2/x)
Um die Dimensionen auszugleichen, bildet man O³/V².
O³=[2*pi*r²(1+2/x)]³=8*pi³r6(1+2/x)³=[8*pi³r6(x+2)³]/x³
V²=[2*pi*r³/x]²=4*pi²*r6/x² 
O³/V²=2*pi*(x+2)³/x
Die Funktion f(x)=(x+2)³/x hat nach der Quotientenregel die Ableitung f '(x)=[2(x+2)²(x-1)]/x². 
Die einzige positive Nullstelle ist x=1, und sie ist eine Tiefstelle. 
Das bedeutet, dass O³ und damit O in x=1 ein Minimum hat. Gleichzeitig hat an der gleichen Stelle V² und damit V ein Maximum, da das Volumen im Nenner steht. 

Es folgen weitere entsprechende Aufgaben auf dieser Seite

Aufgabe 01

Aufgabe 22

Aufgabe 14

Aufgabe 23

Aufgabe 36

Aufgabe 39

Extremwertaufgaben im Internet       top

Deutsch

Dieter Heidorn
Extremwertprobleme mit Nebenbedingungen

Martin Wohlgemuth  (Matroid)
Lösung von Extremwertaufgaben mit Differentialrechnung

MATHEMATIK ONLINE
Extremwert: mit Nebenbedingungen

Wikipedia
Extremwert

Englisch

Duane Kouba 
MAXIMUM/MINIMUM PROBLEMS

Eric W. Weisstein (MathWorld)
First Derivative Test, Second Derivative Test, Extremum Test

Mathalino.com
Steps in Solving Maxima and Minima Problems

Wikipedia
Maxima and minima, Second derivative test,  Higher-order derivative test

Referenzen top
(1) Reinhardt-Zeisberg: Mathematisches Unterrichtswerk Teil IV, Frankfurt a.M. 1938
(2) Lambacher/Schweizer: Analysis, Stuttgart 1954, Seite 94ff, Seite 108 ff.

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  Jürgen Köller 2011

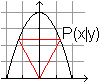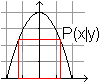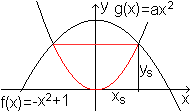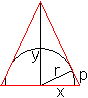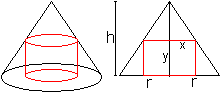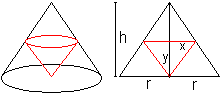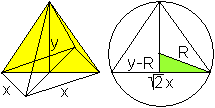
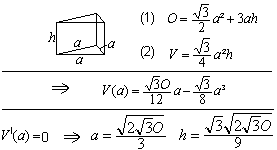
top