The Kaprekar Number 
and more playings with numbers
Contents of this Page
What is the Kaprekar Number? 
The 3n+1 Problem
The Steinhaus Cyclus
The 196-Problem
The Number 1089		 The Number 222
The Number 2997
Kaprekar Number on the Internet
References
.
To the Main Page      "Mathematische Basteleien"

What is the Kaprekar Number? 
The number 6174 is called the Kaprekar number. The Indian mathematician D.R.Kaprekar made the following discovery in 1949.

(1) Take a four-digit number with different digits (acbd with .a<b<c<d)..
(2) Form the largest and the smallest number from these four digits (dcba and abcd)..
(3) Find the difference of these digits. Maybe this is 6174 (dcba - abcd = 6174?).
If it is not, form the largest and the smallest  number from the difference and subtract these numbers again. You may have to repeat this procedure.
The end result is always 6174, but there are no more than 7 steps.
1st example: Take the number 1746.
1st step:  7641 - 1467 = 6174
2nd example: Take the number 5644. 
1st step:  6544 - 4456 = 2088 
2nd step:  8820 - 0288 = 8532 
3rd step:  8532 - 2358 = 6174
3rd example: Take the number  7652. 
1st step:  7652 - 2567 = 5085 
2nd step:  8550 - 0558 = 7992 
3rd step:  9972 - 2799 = 7173 
4th step:  7731 - 1377 = 6354 
5th step:  6543 - 3456 = 3087 
6th step:  8730 - 0378 = 8352 
7th step:  8532 - 2358 = 6174
The problem is solved. (Spektrum der Wissenschaft, Erstausgabe 1978)
Manick Srinivasan and Ramkumar Ramamoorthy sent me more computer results: If you allow numbers with noughts at the beginning like 0342 or 0045, then the Kaprekar number fits for any four digit number except for 1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888, 9999.
They counted the numbers with the same steps:
There totally are 8991=9000-9 four digit numbers.

The 3n+1 Problem (Collatz Problem)  top
Take any natural number, from which you derive a sequence of numbers according to the following rules.
If the number is even, the next number is half of it. If the number is odd, you have to treble it and add 1. This is the next number. Strangely enough this sequence always ends with the number 1. 

1st example: The first number is 16. 
Sequence: 16, 8, 4, 2, 1
2nd example: The first number is 15. 
Sequence: 15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20,10, 5, 16, ,8 ,4 ,2 ,1
3rd example: If you begin with 77 671, you reach 1,570,824,736 as the biggest number. In the end you reach 1 after 232 steps.
The problem has not been solved. (Spektrum der Wissenschaften 4/1984)

The Steinhaus Cyclus top
The Steinhaus Cyclus is 145, 42, 20, 4, 16, 37, 58, 89.

(1) Take any natural number with 4 digits. (abcd)
(2) Add the squares of the digits. (a²+b²+c²+d²)

Handle this sum in the same way. Repeat this calculation.
This procedure comes either to 1 or inevitably to number 145. 
Then the cyclus 42, 20, 4, 16, 37, 58, 89, 145 repeats.

1st example: Take the number 4363.
Sequence: 70, 49, 97, 130, 10, 1, 1, 1, 1,...
2nd example: Take the number 9583.
Sequence: 179, 131, 11, 2, 4, 16, 37, 58, 89, 145, 42, 20, 4, 16, 37, 58, 89, 145, 42, 20, 4, 16, 37, 58, 89, ...
This theorem is proven in Steinhaus' book (3) on 3.5 pages.

The 196-Problem   top
(1) Take any number with three digits (abc)..
(2) Form a mirror number by reversing the digits (cba).
(3) Add the number and its mirror number (abc+cba).

Perhaps the sum is a palindromic number. (This is a number, which doesn't change, if you read it in reverse.)
If it is not a palindromic number, add the mirror number of the sum and the sum itself. Perhaps it is a palindromic number now. Otherwise you have to repeat this procedure. 

In the end nearly all numbers lead to a palindromic number. 

1st example: The number 49 is given.
1st sum:      49 + 94 = 143 
2nd sum:     143 + 341 = 484
Result: 484 is a palindromic number.
2nd example: The number 88 is given. 
1st sum:    88 + 88 = 176 
2nd sum:  176 + 671 = 847 
3rd sum:   847 + 748 = 1595
4th sum:   1595 + 5951 = 7546
5th sum:   7546 + 6457 = 14003 
6th sum:   14003 + 30041 = 44044
Result: 44044 is a palindromic number. 
There are quite a lot of numbers, which don't seem to lead to palindromic numbers. 
The smallest is 196. There is no proof for this statement.

The Number 1089   top
(1) Take any number with three different digits (abc).
(2) Form the mirror number by reversing the digits (cba).
(3) Subtract the number and the mirror number (|abc-cba|).
(4) Add the difference and its mirror number (difference=def, def+fed). 
The result is 1089. 
Take any number with three different digits.

1st example: 
(1) 836
(2) 638
(3) |836-638| = 198
(4) 198+891 = 1089
2nd example (Rakesh):
(1) 536
(2) 635
(3) |536 - 635| = 099
(4) 099+990 = 1089
The proof can be found through elementary mathematics.
Source:  (1) Page 16f. 

The number 222   top
(1) Take any number with three different digits (abc).
(2) Form 5 more numbers by changing the digits in each way (abc, acb, bac, bca, cba, cab).
(3) Add these six numbers (abc+acb+bac+bca+cba+cab). .
.
You get 222-times the sum of the digits, independent on the chosen number [222*(a+b+c+d)].

Example: Take 369. There are the five numbers 396, 639,693, 936, 963 belonging to 369.
The sum is 3996 =  222x(3+6+9).
The proof can be found through elementary mathematics.
You can formulate this problem for numbers with n digits.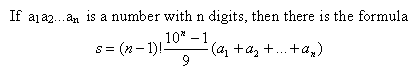
Source: (1) Page 29f.

The Number 2997 top
Mr. Pfiffig (2, Page 75) knows a trick. 
"Tell me three numbers with 3 digits (black below) without 0. I also tell you three numbers (below blue). If we add these six numbers, the result always is 2997." 
Three examples:
  724
+196 
+732
+803
+267
+275
----
2997
  166
+456
+822
+177
+543
+833
----
2997
  111
+555
+888
+888
+444
+111
----
2997
Do you recognize Pfiffig's trick? 

Kaprekar Number on the Internet        top

English

Alfred.Wassermann
Experiments with the 3n+1 sequence   (Applet)

Douglas E. Iannucci
The Kaprekar Numbers
6174 ist die Kaprekar-Zahl. Es gibt auch noch die Kaprekar-Zahlen. 
Beispiel: 494 und 209   (703² = 494209 und 494+209=703)

Eric W. Weisstein (world of mathematics)
Kaprekar Number,   Kaprekar Routine,  196-Algorithm

google.com (Web directory)
Collatz problem    (3n+1-Problem) 

Math Fun Facts (Francis Su) 
Kaprekar's Constant

Terry Trotter
KAPREKAR-6174

Wikipedia
Kaprekar number, Collatz Problem, 196 problem, 

Yutaka Nishiyama
Mysterious number 6174

Deutsch

Alfred.Wassermann
Experiment mit der 3n+1 Folge   (Applet)

KOW’s Blog
1089

Mathetreff 
Aufgabe 1

Gomeck
Schockierende Welt der Zahlen

Wikipedia
Collatz-Problem, Lychrel-Zahl

Winfrid Krone 
Strukturen in einigen künstlichen Zahlenfolgen

References top
(1) Walter Lietzmann: Sonderlinge im Reich der Zahlen, Bonn 1948
(2) Walter Sperling: Auf du und du mit Zahlen, Rüschlikon-Zürich 1955
(3) Hugo Steinhaus, 100 Aufgaben, Urania-Verlag Leipzig, Jena, Berlin 1968

Feedback: Email address on my main page

This page is also available in German

URL of my Homepage:
https://www.mathematische-basteleien.de/

©  2000 Jürgen Köller

top