|
Was ist ein Sehnenviereck?
... ... ... |
Ein Sehnenviereck ist ein Viereck mit einem Umkreis.
Ein Sehnenviereck entsteht, wenn man vier verschiedene
Punkte eines Kreises miteinander verbindet.
Die Seiten sind Sehnen des Kreises. So erklärt sich
der Name. |
... ... ... |
Nach der Definition ist auch ein überschlagenes
Viereck ein Sehnenviereck.
Auf dieser Seite wird vorausgesetzt, dass das Sehnenviereck
konvex ist. |
Satz des Ptolemäus
top
Dieser Satz gibt eine einfache
Beziehung zwischen den Seiten und den Diagonalen eines Sehnenvierecks an.
...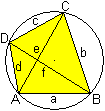 ... ... |
Er lautet:
Das Produkt der Längen der Diagonalen ist gleich
der Summe der Produkte der Längen gegenüberliegender Seiten.
In der Formelsprache heißt das ef=ac+bd. |
Beweis:
...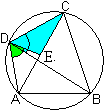 ... ... |
Dazu trägt man den blauen Winkel BDC, der zwischen
einer Seite und einer Diagonalen liegt, an der Seite AD in D nach innen
hin ab. Man erhält die Strecke DE. |
Die Diagonale BD zerlegt
das Viereck in zwei Dreiecke. Zu diesen Dreiecken gibt es zwei ähnliche:
Das Dreieck AED ist dem Dreieck BDC ähnlich, denn
die Dreiecke stimmen in zwei Winkelgrößen überein.
... ... ... |
Die farblich gekennzeichneten Winkel in D sind laut Konstruktion
von E gleich groß.
Die rot gekennzeichneten Winkel sind als Umfangswinkel
über demselben Bogen CD gleich.
Wegen der Ähnlichkeit der Dreiecke gilt die Proportion
e1:d=b:f oder e1f=bd. |
Das Dreieck ABD ist dem Dreieck
ECD ähnlich, denn die Dreiecke stimmen in zwei Winkelgrößen
überein.
...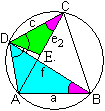 ... ... |
Der blaue und der grüne Winkel in D sind gleich
groß, weil beide Winkel von oben um den gleichen Winkel BDE verringert
wurden.
Die roten Winkel sind als Umfangswinkel über demselben
Bogen AD gleich.
Wegen der Ähnlichkeit der Dreiecke gilt die Proportion
e2:c=a:f oder e2f=ac. |
Addiert man beide Seiten der Produktgleichungen, so ergibt
sich e1f+e2f=bd+ac oder ef=bd+ac, wzbw.
Der Satz ist umkehrbar:
Gilt in einem Viereck die Beziehung ef=ac+bd, so liegen
die Eckpunkte des Vierecks auf einem Kreis und das Viereck ist ein Sehnenviereck.
Anders ausgedrückt:
Die Ptolemäische Ungleichung
lautet: ac+bd>=ef. Nur im Falle des Sehnenvierecks gilt das Gleichheitszeichen.
Vierecke aus
vier Teilen top
...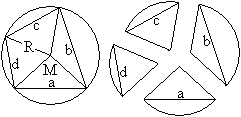 ... ... |
Zeichnet man die Radien des Umkreises durch die vier
Eckpunkte des Sehnenvierecks, so ergibt sich eine Aufteilung in vier Kreisausschnitte. |
Diese Kreisausschnitte kann man zu fünf neuen Sehnenvierecken
zusammensetzen.
 Erstaunlicherweise ergeben sich nur drei verschiedene Diagonalen.
Neben den üblichen Diagonalen e (rot) und f (blau) taucht noch die
Diagonale g (grün) auf.
Erstaunlicherweise ergeben sich nur drei verschiedene Diagonalen.
Neben den üblichen Diagonalen e (rot) und f (blau) taucht noch die
Diagonale g (grün) auf.
Unterhalb der Figuren stehen die Formeln nach dem Satz
des Ptolemäus. Das sind ef=ac+bd, fg=ab+cd und eg=ad+bc.
Bildet man ef*eg/fg, so erhält man e²=(ac+bd)(ad+bc)/(ab+cd)
oder e=sqrt[(ac+bd)(ad+bc)/(ab+cd)].
ef*fg/eg ergibt f=sqrt[(ac+bd)(ab+cd)/(bc+ad)],
fg*eg/ef ergibt g=sqrt[(ab+cd)(ad+bc)/(ac+bd)]
Liegt der Mittelpunkt des
Umkreises außerhalb des Vierecks, so ist die folgende Überlegung
möglich.
...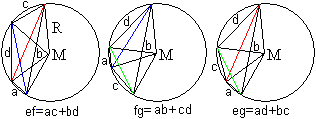 ... ... |
Man teilt den Kreisausschnitt zu b auf dreierlei Weise
auf.
So gelangt man zu denselben Formeln wie oben. |
Winkelsatz
top
|
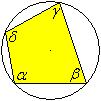
Es gilt der Satz =>:
Im Sehnenviereck gilt alpha+gamma=180°
und beta+delta=180°.
In Worte: Gegenüberliegende
Winkel ergänzen sich zu 180°. |
Die Aussage ist umkehrbar <=:
Ist in einem Viereck die Summe
gegenüberliegender Winkel 180°, so ist es ein Sehnenviereck.
Beweis
für die Richtung =>:
Es wird der Satz "Der
Umfangswinkel ist halb so groß wie der zugehörige Mittelpunktswinkel"
vorausgesetzt.
... ... ... |
Dann gilt beta=epsilon/2 und delta=epsilon'/2, außerdem
ist epsilon+epsilon'=360°.
Daraus folgt beta+delta=epsilon/2+epsilon'/2=(epsilon+epsilon')/2=360°/2=180°
wzbw..
Die Winkelsumme im Viereck ist 360°. Deshalb gilt
alpha+gamma=180°.
Liegt der Kreismittelpunkt M außerhalb des Vierecks,
gilt eine ähnliche Rechnung. |
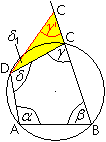
Beweis
für die Richtung <=:
... ... ... |
...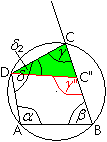 ... ... |
Angenommen, C liege außerhalb des Kreises und hieße
C'. Dann gilt im gelben Dreieck nach dem Satz von den Außenwinkeln
gamma=gamma'+delta1
e. Daraus folgt alpha+gamma'<180°.
Angenommen, C liege innerhalb des Kreises und hieße
C''. Dann gilt im grünen Dreieck nach dem Satz von den Außenwinkeln
gamma''=gamma+delta2. oder gamma=gamma''-delta2.
Daraus folgt alpha+gamma''>180°. |
Ergebnis: Nur wenn alpha+gamma=180°
ist, liegt der Punkt C auf der Kreislinie.
Berechnungen
top
Ein beliebiges Viereck ist im Allgemeinen durch fünf
Größen festgelegt. Drei Größen legen ein Dreieck
fest. Mit dem Dreieck ist auch sein Umkreisradius gegeben. Für einen
vierten Punkt genügt eine weitere Größe. Also ist zu vermuten,
dass ein Sehnenviereck immer durch
vier passende Größen
festgelegt wird.
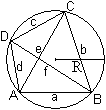
Der Normalfall ist wohl, dass die vier Seiten a,
b, c und d gegeben sind.
... ... ...
|
Dann stellt sich das Problem, die übrigen Größen
zu berechnen.
Das sind u.a.
Umfang
U, Hauptdiagonale e, Nebendiagonale
f,
Radius R des Umkreises und Flächeninhalt A
|
Es gilt
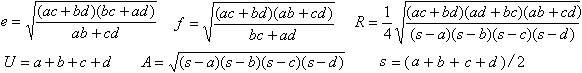
Die Formel für den Flächeninhalt heißt
Formel des Brahmagupta.
Zur den Formeln und ihren
Herleitungen
Diagonalen
...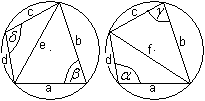 ... ... |
Nach dem Kosinussatz e²=a²+b²-2ab*cos(beta)
und e²=c²+d²-2cd*cos(delta).
Es gilt cos(delta)=cos(180°-beta)=-cos(beta) und
e²=c²+d²+2cd*cos(beta).
cos(beta) wird eliminiert: (a²+b²-e²)/(2ab)=(c²+d²-e²)/(2cd).
Daraus folgt e²=(ac+bd)(ad+bc)/(ab+cd) oder e=sqrt[(ac+bd)(ad+bc)/(ab+cd)].
Analog erhält man f²=(ac+bd)(ab+cd)/(bc+ad)
oder f=sqrt[(ac+bd)(ab+cd)/(bc+ad)]. |
Es gilt weiter e²f²=(ac+bd)(ad+bc)/(ab+cd)*(ac+bd)(ab+cd)/(bc+ad)=(ac+bd)²
und ef=ac+bd.
Damit wird ein weiterer Beweis des Satzes von Ptolemäus
erbracht.
Ferner gilt e² : f²
= [(ac+bd)(ad+bc)/(ab+cd)] : [(ac+bd)(ab+cd)/(bc+ad)] = (ad+bc)² :
(ab+cd)² oder
e : f= (ad+bc) : (ab+cd).
Umfang
Der Umfang ist U=a+b+c+d.
Interessant
ist, dass von allen Vierecken mit den Seiten a,b,c und d das Sehnenviereck
den größten Umfang hat.
Flächeninhalt
...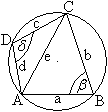 ... ... |
Die Diagonale e teilt das Viereck in zwei Dreiecke auf.
Für die Flächen gilt:
A=A1+A2=ab/2*sin(beta)+cd/2*sin(delta)=ab/2*sin(beta)+cd/2*sin(180°-beta)
und schließlich
(#) A =[(ab+cd)/2]*sin(beta)
Andererseits gilt nach dem Kosinussatz e²=a²+b²-2abcos(beta)
und e²=c²+d²-2cd*cos(delta) oder
(##) a²+b²-c²-d²=2(ab+cd)cos(beta). |
Die Terme beider Gleichungen werden quadriert:
(#) A² =(ab+cd)²/4*sin²(beta) und (a²+b²-c²-d²)²=4(ab+cd)²cos²(beta).
Für cos²(beta) kann man noch 1-sin²(beta) setzen:
(##) (a²+b²-c²-d²)²=4(ab+cd)²[1-sin²(beta)]
und erhält sin²(beta)=[4(ab+cd)²-(a²+b²-c²-d²)²]/4(ab+cd)².
Diesen Ausdruck setzt man in A² =(ab+cd)²/4*sin²(beta) ein
und erhält 16A²=[4(ab+cd)²-(a²+b²-c²-d²)².
Ausmultipliziert ergibt sich
(###) 16A²=2a²b²+2a²c²+2a²d²+2b²c²+2b²d²+2c²d²-a4-b4-c4-d4+8abcd.
Dieser Ausdruck muss zu A=sqrt[(s-a)(s-b)(s-c)(s-d)]
mit s=(a+b+c+d)/2 führen. Setzt man s ein und quadriert, erhält
man
16A²=(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d). Dieses
Produkt wird ausmultipliziert und man erhält am Ende den Term (###).
Wenn man noch die letzte Rechnung wegen des logisch richtigen
Aufbaus umkehrt, ist die Formel bewiesen.
Diese Herleitung findet man im
Prinzip bei Dr.Math, andere Herleitungen bei en.wikipedia, bei Jim Wilson
oder bei Hartmut Wellstein (URLs unten).
Für beliebige Vierecke
gilt die Formel von Bretschneider A=sqrt[(s-a)(s-b)(s-c)(s-d)-abcd*cos²((alpha+gamma)/2]
mit s=(a+b+c+d)/2 .
Setzt man sie voraus und setzt alpha+gamma=180°,
so ergibt sich auch die obige Formel A=sqrt[(s-a)(s-b)(s-c)(s-d)] als Sonderfall.
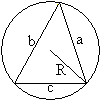
Radius
des Umkreises
...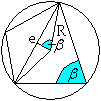 ... ... |
Nach dem Satz "Der Mittelpunktwinkel ist doppelt so groß
wie der Umfangswinkel" kann man sin(beta)=(e/2)/R ablesen.
Andererseits gilt die Formel (#) A=[(ab+cd)/2]*sin(beta)
von oben.
Man eliminiert sin(beta) und erhält A=(ab+cd)/2*(e/2)/R.
Daraus folgt R=[(ab+cd)/2*(e/2)]/A. |
Setzt man e=sqrt[(ac+bd)(ad+bc)/(ab+cd)] und A=sqrt[(s-a)(s-b)(s-c)(s-d)]
ein, so erhält man die gesuchte Gleichung R=sqrt{[(ac+bd)(ad+bc)(ab+cd)]/[(s-a)(s-b)(s-c)(s-d)]}/4.
Verschiedenes
top
Aufteilung in Vierecke
...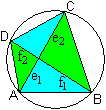 ... ...
|
Die beiden Diagonalen teilen das Sehnenviereck in vier
Teildreiecke auf.
Es gilt: Je zwei gegenüberliegende Dreiecke sind
ähnlich.
Daraus lässt sich eine Beziehung zwischen den Diagonalenabschnitten
ablesen.
e1 : f1 = f2
: e2
|
Man kann die Gleichung auch als Produktgleichung schreiben:
e1e2
= f1f2 . Das ist der Sehnensatz
Dann kann man zum Beispiel die Aufgabe lösen zu
einem Rechteck ein flächengleiches Rechteck zu konstruieren.
Beweis:
...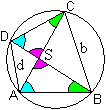 ... ... |
Die Dreiecke ABS und CDS sind ähnlich.
Sie stimmen in drei Winkeln überein, nämlich
in den Scheitelwinkeln und den Umfangswinkeln über den Sehnen BC und
AD.
Wegen der Ähnlichkeit gilt die Proportion
e1 : f1 = f2 :
e2. |
Sehnenvierecke
unter den Standard-Vierecken
...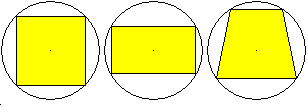 ... ... |
Die nebenstehenden bekannten Vierecke sind auch Sehnenvierecke.
Es sind das Quadrat, das Rechteck und das gleichschenklige
Trapez.
|
Eigentlich müsste das Quadrat nicht aufgeführt
werden, da jedes Quadrat auch ein Rechteck ist.
In alten Büchern gab es für Rechtecke, die
kein Quadrat sind, einen Namen. Sie hießen die Oblongen (Einzahl
das Oblongum).
Heute steht im neuen Duden nur noch das Wort oblong mit
der Beschreibung "veraltet für länglich, rechteckig".
Drachenviereck
...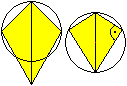 ... ...
|
Das Drachenviereck hat im Allgemeinen keinen Umkreis,
wenn aber die gleichen Winkel des Drachens rechte Winkel sind, ist der
Drachen auch ein Sehnenviereck.
Man erkennt den Halbkreis des Thales. |
Sehnentangentenviereck
Das Quadrat hat als Sehnenviereck eine zusätzliche
Eigenschaft: Es hat auch einen Inkreis.
Die Mittelpunkte von In- und Umkreis fallen zusammen.
...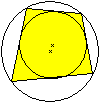 ... ... |
Es gibt auch andere Sehnenvierecke, die einen Inkreis
haben.
Die Mittelpunkte können wie links verschieden sein.
Die Seiten des Sehnenvierecks werden zu Tangenten und
das Viereck ist dann auch ein Tangentenviereck. |
Ein Viereck mit In- und Umkreis heißt
Sehnentangentenviereck.
Ein
Rechteck im Sehnenviereck
...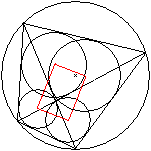 ... ...
|
Jede Diagonale teilt das Sehnenviereck in zwei Dreiecke
auf. Es entstehen vier Dreiecke.
Verbindet man die Mittelpunkte der vier Inkreise, so ergibt
sich ein - Rechteck. |
Einen Beweis findet man bei Antonio Gutierrez unter dem Stichwort
Sangako Problem (URL unten)
Bitte den Lautsprecher einschalten :-).
Butterfly
Theorem
...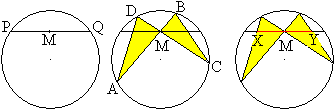 ... ... |
1 Zeichne einen Kreis und die Sehne PQ mit dem Mittelpunkt
M.
2 Zeichne durch M zwei beliebige Sehnen und ergänze
die Figur zu einem überschlagenen Sehnenviereck.
3 Es gilt: Die so entstehende Strecke XY wird durch M
halbiert. |
Einen Beweis findet man bei Antonio Gutierrez.
Über
Abstände
...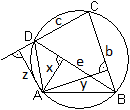 ... ... |
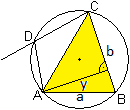
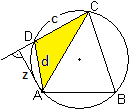
Fällt man vom Eckpunkt A aus Lote auf die gegenüberliegende
Diagonale und auf die gegenüberliegenden Seiten und nennt die Lote
x, y und z, so gilt
BD/x = BC/y+CD/z oder e/x = b/y+c/z.
|
Beweis
...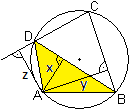 ... ... |
Das Dreieck ABD hat den Flächeninhalt A = (1/2)BD*x. |
...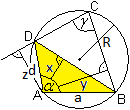 ... ... |
Eine andere Formel für den Flächeninhalt des
Dreiecks ABD ist A = (1/2)ad*sin(alpha).
Für den Radius des Umkreises des Dreiecks ABD gilt
R = (1/2)BD/sin(alpha). Daraus folgt sin(alpha) = BD/(2R).
Das setzt man in die Flächenformel ein: A = (1/2)ad*BD/(2R)
oder A = (1/4)ad*BD/R. |
Aus den Formeln A = (1/2)BD*x
und A = [(1/4)ad*BD]/R ergibt sich x = (ad)/(2R).
Es gilt weiter BD/x = (2R*BD)/(ad).
In Analogie zu dieser Formel gelten auch
...
...BC/y = (2Rb)/(a*AC) |
CD/z = (2Rc)(d*AC) |
Man geht von der zu beweisenden
Formel aus und setzt ein.
BD/x = BC/y+CD/z
<=> (2R*BD)/(ad) = (2Rb)/(a*AC)+(2Rc)/(d*AC)
<=> (2R*BD)/(ad) = (2Rb)/(a*AC)+(2Rc)/(d*AC)
|/(2R) |*ad
<=> BD*AC = bd+ac
Man erhält den Satz des Ptolemäus. Da die letzten
Rechenschritte umkehrbar sind, ist der Beweis geführt.
Quelle: https://www.cut-the-knot.org/m/Geometry/IdentityInCyclicQuadrilateral.shtml
Brahmagupta-Vierecke.
In Analogie zu den Pythagoräischen Dreiecken gibt
es Brahmagupta-Vierecke.
Pythagoräische Dreiecke sind rechtwinklig und ihre
Seitenlängen sind natürliche Zahlen.
Das einfachste Dreieck ist das 3-4-5-Dreieck.
Entsprechend hat man nach Sehnenvierecken gesucht, die
neben ganzzahligen Seiten auch ganzzahlige Diagonalen und Flächen
haben. Ein Beispiel ist a=65, b=25, c=33, d=39, e=60, f=52, A=1344.
Zu diesem Problem gibt es im Internet eine Untersuchung
von K.R.S.Sastry (URL unten).
Weitere
Vielecke mit Umkreis top
Dreiecke
|
Jedes Dreieck hat einen Umkreis. Deshalb ist jedes Dreieck
ein Sehnendreieck. |
Bestimmte Dreieckssätze haben bei den Sehnenvierecken
Entsprechungen:
Dreieck: Heron-Formel A=sqrt[s(s-a)(s-b)(s-c)] mit s=(a+b+c)/2
Viereck: Brahmagupta-Formel A=sqrt[(s-a)(s-b)(s-c)(s-d)]
mit s=(a+b+c+d)/2 |
Dreieck: A= abc/(4R)
Viereck: A=efg/(4R) |
Vielecke
mit Umkreis
... ... ...
|
Alle regelmäßigen Vielecke haben einen Umkreis
und man könnte sie als "Sehnenvielecke". bezeichnen.
Sie haben auch einen Inkreis und zählen auch zu
den "Tangentenvielecken". |
Sehnenfünfeck
Bei Mathworld (Cyclic Pentagon) - nicht mehr online -konnte
man nachlesen, dass das Fünfeck sich nur schwer erschließt.
So ist zum Beispiel der Flächeninhalt die Lösung
einer komplizierten Gleichung 7. Grades.
Sehnensechseck
Zum Sehnensechseck folgen noch zwei Aussagen.
...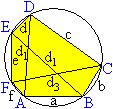 ... ... |
Gegeben sind ein konvexes Sehnensechseck und die drei
Diagonalen, die jeden dritten Eckpunkt miteinander verbinden.
Dann gilt d1d2d3=ebd1+cfd2+add3+ace+bdf.
Das ist eine Übertragung des Satzes von Ptolemäus
auf ein Sechseck. |
Man findet den Satz im Internet in Suchmaschinen mit den
Suchwort "Fuhrmann's theorem".
Ein
Winkelsatz
...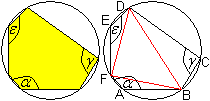 ... ... |
Satz: Im Sehnensechseck ist die Summe nichtbenachbarter
Winkel 360°.
Beweis: Das Viereck ABDF ist ein Sehnenviereck, so dass
der Winkel bei D im roten Dreieck gleich 180°-alpha ist. Entsprechend
gilt für die übrigen Winkel 180°-gamma und 180°-epsilon. |
Die Winkelsumme ist 180°:
(180°-alpha)+(180°-gamma)+(180°-epsilon)=180°.
Daraus folgt die Behauptung alpha+gamma+epsilon=360°.
Sehnenviereck
im Internet top
Deutsch
Arne Madincea
Der
Flächeninhalt eines Sehnenvierecks (.pdf-Datei)
Eckard Specht (math4U)
Tangentenviereck
(7 Aufgaben mit Lösungen), Sehnenviereck
(8 Aufgaben mit Lösungen)
Sehnentangentenviereck
(1 Aufgabe mit Lösung)
Universität Bayreuth Lehrstuhl
für Mathematik und ihre Didaktik
Unterrichtssequenz
'Sehnenviereck' (Geonet)
Wikipedia
Sehnenviereck,
Tangentenviereck,
Japanischer
Satz für Sehnenvierecke, Satz
von Ptolemäus
Englisch
Alexander Bogomolny (cut-the-knot)
Identity
In Cyclic Quadrilateral
Eric.W.Weisstein
Cyclic
Quadrilateral, Ptolemy's
Theorem, Ptolemy
Inequality, Bretschneider's
Formula, Fuhrmanns
Theorem,
Cyclic
Pentagon,
Cyclic
Hexagon,
Cyclic
Polygon, Lemoine
Hexagon, Butterfly
Theorem
Jim Wilson
Brahmagupta's
formula
K.R.S.Sastry (Forum Geometricorum)
Brahmagupta
Quadrilaterals (.pdf-Datei)
Wikipedia
Cyclic
quadrilateral, Ptolemy's
theorem, Circumcircle,
Brahmagupta's
theorem,
Japanese
theorem for cyclic quadrilaterals
Referenzen top
(1) Hahn/Dzewas: Mathematik 8.Schuljahr, Braunschweig
1990 [ISBN 3-14-112958-4]
(2) Peter Baptist: Pythagoras und kein Ende? Leipzig
1998 [ISBN 3-12-720040-4]
(3) Theo Kühlein: Ebene Trigonometrie II, Mentor-Repetitionen,
Berlin 1962 (7th ed.1974) [ISBN 3-580-63140-3]
(4) Martin Mettler: Vom Charme der 'verblassten' Geometrie,
Timisoara, (2000) Rumänien [ISBN 973-9441-97-1]
(5) Alfred S. Posamentier, Charles T. Salkind: Challenging
Problems in Geometry, Dover Publications, 1996
Viele Tipps und die drei letzten Literaturangaben
stammen von Torsten Sillke.
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |

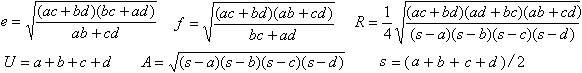
 ...
... ...
... ...
... ...
... ...
... ...
...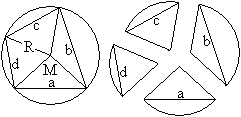 ...
... ...
...
 ...
... ...
... ...
... ...
...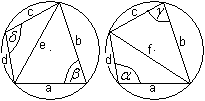 ...
... ...
...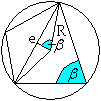 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...


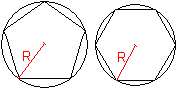 ...
... ...
... ...
...