|
What is a Tetracube?
 Figures, which are made of four cubes,
are called tetracubes. There are eight possibilities.
Figures, which are made of four cubes,
are called tetracubes. There are eight possibilities.
Five figures are in the plane,
three are three-dimensional.
The tetracubes are called I, O,
L, T, N, tower right, tower left and tripod.
If you leave out the 1x4 bar and
the 2x2 square and add the V-piece with three cubes, you get the seven
Soma cubes. I made a web site about this topic.
Building
Rectangular Solids of Tetracubes top
The tetracubes have 32 cubes altogether.
- There is 32=2x4x4.
... ... ... |
... ... ... |
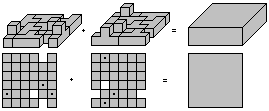
So you have the problem to form a rectangular solid 2x4x4
of all the tetracubes. There are 1390 possibilities, as a group of scientists
at the MIT found out with the help of a computer (2). |
... ... ... |
... ... ... |
Another product of 32 is 2x2x8. The company Lowe Co.
sold the tetracube shaped 2x2x8 called "The Wit's Puzzle" in Hongkong in
1967 (2). |
The 2x2x8 solid is formed by one 2x2x4-, one 2x2x3- und one
2x2x1-solid.
More
3-D-Shapes from Tetracubes top
You can look for shapes from 32
cubes and build them with tetracubes.
... ... ...
|
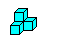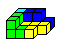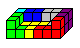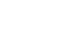
|
Here is a bathtub as an example, designed and solved. |
More (soluble) plans: Well, bed, penthouse,
tower, settee, cube and cross, figure with column
Skyline
top
Here I publish one of Victor Stok's tetracube results.
He worked e.g. on all figures with four equal layers you can build with
all tetracubes. There are 71 figures, which you can distribute to 21 classes.
In the drawing you see figures representing one class.
There is a notation for the figures. Numbers describe
the position of the bars and the height. The figure 12 e.g. has the notation
1223.
Class 1: 11111111
Class 2: 1111112, 1211111,
1121111, 1112111
Class 3: 111113,
11311, 13111
Class 4: 111122,
111212, 112112, 121112, 211112, 111221, 112121, 121121, 112211
Class 5: 11114,
14111, 11411
Class 6: 11123, 11132, 11213,
11231, 11312, 11321, 12113, 12131, 13112, 21113
Class 7: 1115,
1511
Class 8: 11222,
12122, 12212, 12221, 21122, 21212
Class 9: 1124, 1214,
1241, 1412, 2114
Class 10: 1133,
1313, 3113, 1331
Class 11: 116,
161
Class 12: 1223,
1232, 1322, 2123, 2132, 2231
Class 13: 125,
152,
215
Class 14: 134,
143,
314
Class 15: 17
Class 16: 2222
Class 17: 224,
242
Class 18: 233,
323
Class 19: 26
Class 20: 35
Class 21: 44
If the numbers are green,
the building of the figures is possible. Red
means insoluble. Black means, that the figure
is not solved, but it is not proved that there is no solution.
Daniel Moelle detected with the help of his computer
that the four open cases in black have also a solution. I could build the
figures by his instructions.
Magnification Problem
top
You can imitate every tetracube with all eight pieces
in double magnification.
... |
 |
I already introduced the tetracubes I and O as rectangular
solids. |
... ... ... |
... ... ... |
tetracube L... |
... ... ... |
... ... ... |
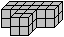
tetracube T |
(Victor Stok's solution)
... ... ... |
You can lay two bicubes.
These bicubes form the left
& right tower, by the way also piece L. |
... ... ... |
... ... ... |
Tripod from eight tetracubes |
(Darian Jenkin's solution)
Ishino Keiichiro has found all the
solutions of the magnification problem.
I:224, O:1390,
L:1804, T:356, N:770, Left & Right Towers
both:803, Tripod:126.
(Communicated by Darian
Jenkins)
Cubes
with Congruent Tetracubes top
I talk about tetracubes the same shape. You can build
cubes for instance.
4x4x4 Cube
... |
Four T-tetracubes form a 4*4-mat. |
Four mats form a 4x4x4 cube.
6x6x6 Cube
... ... ... |
9 T-tetracubes form a 6*6-mat with 3 valleys and 3 mountains. |
... ... ... |
You build the same mat once more, turn it through 90°
and put it over the first one.
Then you have a 2*6*6-box of 18 tetracubes. |
Three 2*6*6-boxes form a cube.

|
My 54 home made tetrominos for the 6x6x6 cube.
(Thank you, Julia) |
4x4x4-Cube top
... ... ... |
A set of tetracubes has 32 cubes. |
... ... ... |
A second set of tetracubes adds up to 64 cubes. |
This leads to the problem to build
a 4x4x4 Cube with all 64 cubes.
Solution, sent by Darian Jenkins
... |
 |
The pairs of the tetracubes L, T, N, and I form half
a 4x4x4 cube. |
... |
...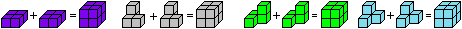 ... ... |
You lay the three-dimensional tetracubes
and O on each other and you have four 2x2x2 cubes or half a 4x4x4 cube. |
The two halves form the 4x4x4 cube.
Tetrominos
top
... ... ...
|
You can also give four squares instead of four
cubes.
Then you only get five tetrominos instead of eight tetracubes. |
...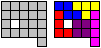 ... ... |
The five tetrominos have 20 squares altogether. But it
is not possible to form a 4x5 rectangular. One square is jutting and a
hole remains. |
... ... ... |
... ... ... |
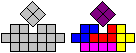
Herbert Fink had the idea to create a 4x6 rectangular
with four holes and a 5x5 squarewith 5 holes.
There is only one solution. |
... ... ... |
Tetrominos are not good to play with.
The number of the pieces is small and the pieces 1x4
and 2x2 are bulky. |
... |
There is a series of 3x7-rectangles with a hole. |
... ... ... |
You can lay a rectangle 8x5 with two sets of tetrominos.
This puzzle was sold as an "Adult Game" ;-) in the series
"Beat the Computer" in the 1970s.
The computer FACOM 270-20 found 783 solutions
(Tenyo Co.,Ltd. Tokyo, Japan). |
Torsten Sillke's Tip
Tetris top
Tetrominos remind on the computer game tetris.
...
...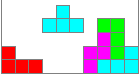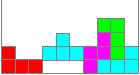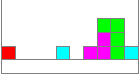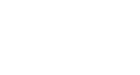 ... ... |
This is the game:
Tetrominos fall down in a box. While falling you must
move the pieces to the right or the left or turn them, so that they form
a horizontal layer with squares. This succeeded in the picture on the left.
The light blue piece closes the gap in the next moment. You get points.
The row of ten squares disappears.
The next RND piece follows.
If there is no full layer of squares, a heap grows. If
the pieces reach the upper edge of the box, the game is finished. The end
is inevitable: The pieces fall faster with the points, in the end so fast,
that you can only watch. |
Tetris has an interesting history: The Russian Alexij
Patschitnow invented it in 1984. He was working in the computer center
of the Academy of Science in Moscow at that time. The game soon became
the student's cult game at Moscow universities. There were also clones
at German universities, which even ran on computers not being able to show
graphics. I remember pieces were made by double crosses (#).
Minoru Arakawa, president of Nintendo of America, watched
the game on a computer fair and bought the rights for commercialization
- cheaply. (There is an own story behind this word.). When the Game Boy
entered the market, it was equipped by this game. Then Tetris really became
famous.
Many different versions of the game were developed for
the PC in the last 25 years. Maybe the shareware game Wintris is the most
well kown. You play it with the cursor keys and key 5.
I recommend two games similar to tetris, the freeware
game Columns and the postcard-ware program ;-) Clickomania. You can download
both games on the internet. Be careful, you can become addicted.
Making
of Tetracubes top
If you want to play with tetracubes
you have to make them with your hands.
You can make tetracubes of cubes. You buy a length of
wood which is square in cross-section, cut it into cubes and glue the cubes
together.
Another method is glueing dice.
The best thing is to use a two component glue, because it needs time to
harden. Then you can form the tetracubes without having to hurry.
A cheap method is making them from a sheet of paper. You
must design a base of every tetracube and fold it.
Tetracubes
on the Internet top
German
Andrew Clarke
Polykuben
Wikipedia
Tetris
English
Andrew Clarke
Polycubes
Torsten Sillke
Quader
aus kongruenten Tetrawürfeln
Wikipedia
Tetromino,
Tetris
References top
(1) Martin Gardner: Mathematical Puzzles & Diversions,
New York 1959
(2) Martin Gardner: Bacons Geheimnis, Frankfurt am Main,
1986 (ISBN 3-8105-0800-4)
(3) R.Thiele, K.Haase: Der verzauberte Raum, Leipzig,
1991 (ISBN 3-332-00480-8)
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |


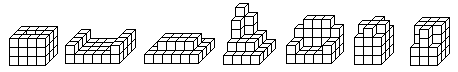
 ...
... ...
... ...
...

 ...
...
 ...
... ...
...