What is a Flexatube?

3D-picture

The aim is to turn inside out by foldings only. 

Folding a sock is a simpler exercise ;-).

The flexatube is a classic among the puzzles and belongs to the flexagons or is related to them. They were found by Arthur H. Stone in the 1930s. They became popular by Gardner's articles and books. 

There are several variations and further developments on flexatubes. You find some at D.Mitchell (1). 

Making of a Flexatube  top
It is simple to build them. 
The colours yellow and grey in the drawings are to support the descriptions.

>Take a white sheet of paper A4. 

......

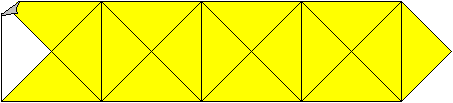>Draw a strip of four squares with the side 5cm and their diagonals as seen on the left.  >Add a quarter square on the right.  >Cut out the strip. >Go over the lines with an empty ball pen in order to  fold the paper at the lines more easily.

>Glue the jutting quarter triangle on the right on the white field on the left. This leads to a ring. 
>Form the cube shape.

Solution    top
1st part
1

Push the front square down horizontally. The blue lines are folds and mountains.

Then it must look like this.

......

Turn over the paper so that the grey square is horizontal.

Fold on the red lines. They are valleys.  In other words: Lay point P on point P'.

Then it must look like this.

......

There is a half square at the reverse side. Turn it backwards so that it is perpendicular to the yellow square.

......

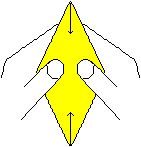
There is a slit in the centre. Widen it in direction of the arrows.

......

This is a drawing of my page about the paper boat. It fits here.  Widen the slit and lay the upper and the lower parts on each other.

Then it must look like this.  There has developed a bag above.

Turn over the paper.  There is also a bag on the reverse side, but the colours have changed.

......

Put your thumbs into the bag and push in the squares on both sides at the red lines with your index finger.

Then it must look like this.  Pull out both x-sheets (meeting in P).

Then it must look like this.  Pull out the horizontal grey square.

You get the solved flexatube in the end.

A Second Solution  top

...... Step 9

There is a simple solution in booklet (1).  The 2nd part (step 11 to 14) is easily to understand:  Put the yellow corner below into the grey bag above and unfold the paper.  1st part: You get step 1 to 9 by retracing the putting in and unfolding. This is not easy.

Flexatubes on the Internet top

English: 

Harold V. McIntosh
General Tetraflexagon, Flexatube, or Bregdoid

NN
David Mitchell's Origami Heaven - Flexagons - A Flexagon Bibliography

Eric W. Weisstein
Flexatube

Comments   top
The flexatube has some features of a good puzzle. 

>It is simple to look at and to make it. 
>Everybody can solve it after some or more minutes. But then you don't know how to repeat the solution. 
>If you want to reproduce the solution, you must recognize structures and go forward systematically. 
>Turning back folds is a principle of this puzzle. This leads to a solution in two parts.
>There are several independent solutions. 

References    top
(1) David Mitchell: The Magic of Flexagons, Norfolk England 1998 (ISBN 1 899618287)
(2) Martin Gardner: The Second Scientific American Book of  Mathematical Puzzles and Diversions, Simon & Schuster (1961)
(3) Martin Gardner: Wheels, Life, and other Mathematical Amusements, Freeman (1983) New York
(3') Martin Gardener: Martin Gardner's mathematische Denkspiele, Hugendubel München 1987 (ISBN 3 88034 323 3) 
      (Die Kombinatorik des Papierfaltens,  Seite 32ff.)