|
Illustrations of Formulas
|
What are Illustrations of formulas?
Formulas are statements of algebra, which apply to numbers
of a definition set.
They can be proved except the axioms. You can deduce new
formulas by well-known formulas by logical reasoning. This procedure is
called a proof.
The proof ideas and also the proof ways can be described
by pictures. In addition the formulas themselves become more alive.
You can find illustrations of well known formulas on
this page.
Simple Formulas
top
Commutative law of multiplication
(Axiom)
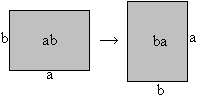
ab=ba
Distributive law (Axiom)
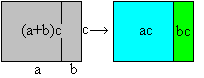
(a+b)c=ac+bc
Product of a difference and a number
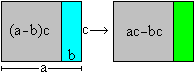
(a-b)c=ac-bc
Product of two sums
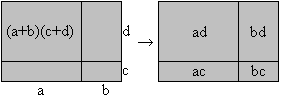
(a+b)(c+d)=ac+ad+bc+bd
Product of two differences
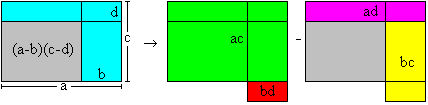
(a-b)(c-d)= ac+bd -ad-bc
Product of a sum and a difference
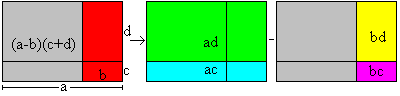
(a-b)(c+d)= ac+ad -bc-bd
Looking for a parallelogram with the same area
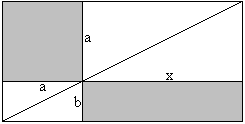
a²=bx
Binomial Formulas
top
First binomial formula
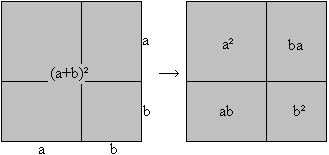
(a+b)²=a² + 2ab + b²
Second binomial formula

(a-b)²= b²+a² -2ab
Third binomial formula
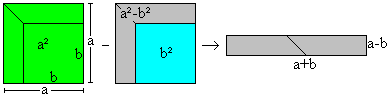
a²-b²=(a+b)(a-b)
Tri-nomial formula
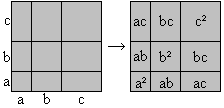
(a+b+c)²=a²+b²+c²+2ab+2ac+2bc
Difference of the squares of a sum and a difference
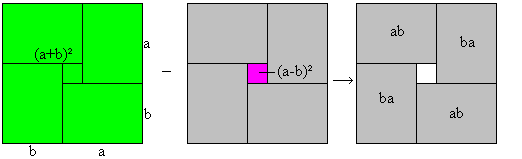
(a+b)²-(a-b)²=4ab
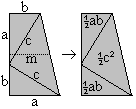
Pythagoras's Theorem
top
The Pythagorean theorem (Pythagoras or one of his students,
Pythagoras of Samos, 580-500 BC)
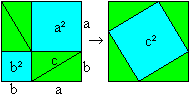
a²+b²=c²
The Pythagorean theorem (Euklid, ~300 BC)
Classical proof with triangles
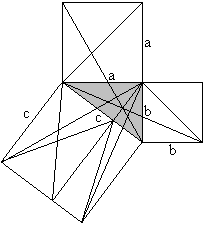 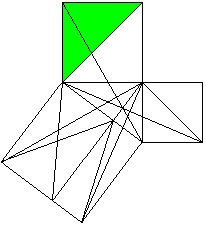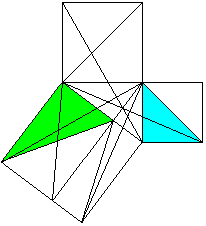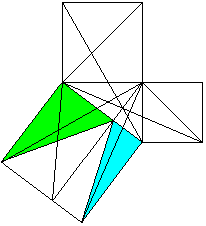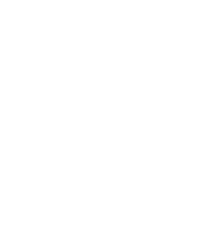
a²+b²=c²
The Pythagorean theorem (Euklid, ~300 BC)
Proof with four-sided figures
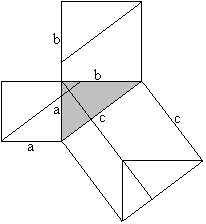 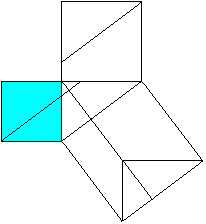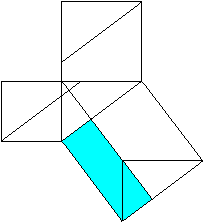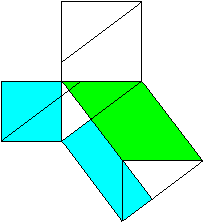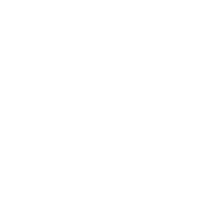
a²+b²=c²
Euklid's theorem (Euklid, ~300 BC)
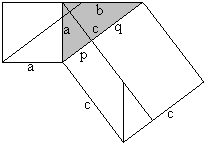 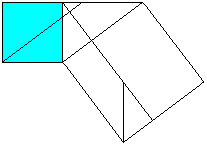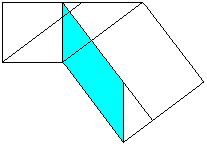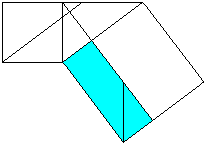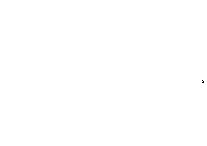
a²=cp (You can show b²=cq in analogy.)
Height formula
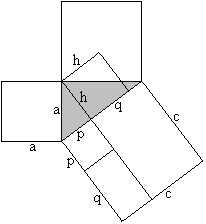 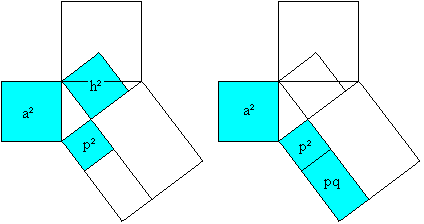
a²=p²+h² (Pythagorean theorem), a²=pc=p²+pq
(Euklid's theorem),
hence h²=pq
The Pythagorean theorem (Liu Hui, ~300, China)
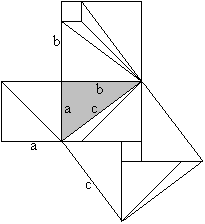 
a²+b²=c²
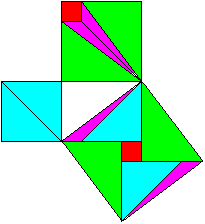
The Pythagorean theorem ("The bride's chair", ~900, India)
a²+b²=c²
The Pythagorean theorem (Atscharja Bhaskara, Indien,
~1150)
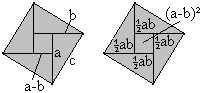
c²=(a-b)²+2ab oder c²=a²+b²
The Pythagorean theorem (Leonardo da Vinci, 1452-1519)
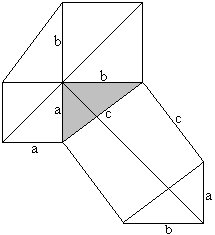 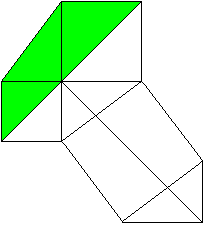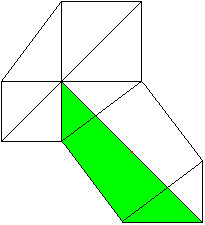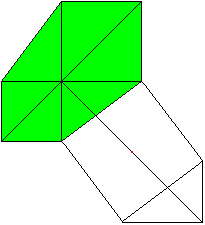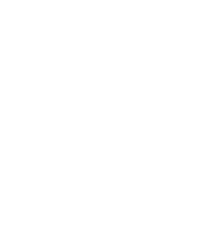
a²+b²=c²
The Pythagorean theorem (Arthur Schopenhauer's case was a=b,
1788-1860)
a²+b²=c²
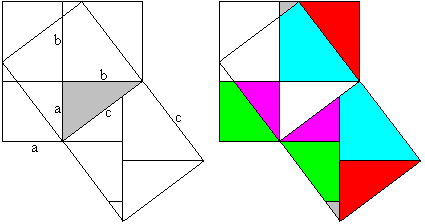
The Pythagorean theorem (James Garfield 1876, later on the
20th US President)
You use the formula of the area of a trapezium [A=mh,
here h=a+b and m=(a+b)/2]
(a+b)²/2=c²/2+2*(1/2*ab) or a²+b²=c²
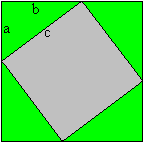
The Pythagorean theorem (Hermann Baravalle 1945)
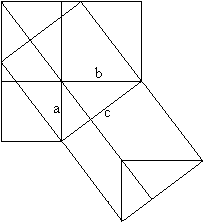 ......... .........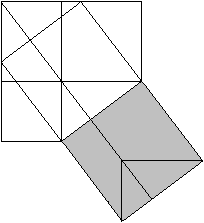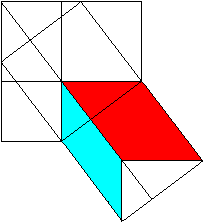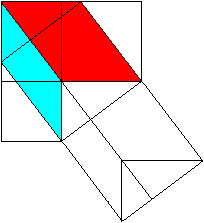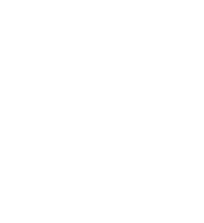
c²=a²+b²
The Pythagorean theorem
(a+b)²=c²+4*(1/2ab) oder a²+b²=c²
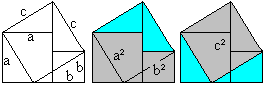
Cubes top
Cube of a sum

(a+b)³=a³+3a²b+3ab²+b³
You can see both cubes and the six rectangular parallelepipeds
in 3D-view:
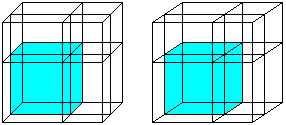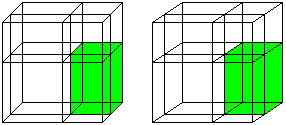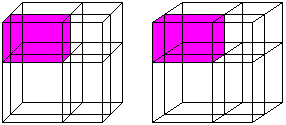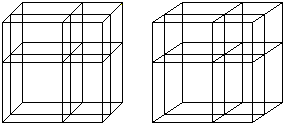
Cube of a difference
The formula is (a-b)³=a³-3a²b+3ab²-b³.
You convert it to (a-b)³=a³-3ab(a-b)-b³ for an illustration.
...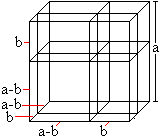 ... ... |
You take the drawing of the formula (a+b)³=a³+3a²b+3ab²+b³
from above and replace a by the difference a-b.
Then the edges are (a-b)+b with different combinations
(on the left).
The term (a-b)³ is illustrated by the blue cube (on
the right).
|
...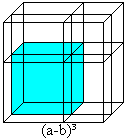 ... ... |
You recieve the blue cube, too, if you take away the
three green bodies and the yellow cube from the red cube:
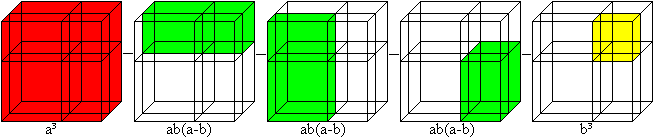
(a-b)³ = a³-3ab(a-b)-b³ = a³-3a²b+3ab²-b³
References
top
Alexander Bogomolny, http://www.cut-the-knot.com/pythagoras
Martin Gardner, Mathematisches Labyrinth, Vieweg Braunschweig
1979 (ISBN 3-528-08402-2)
Johannes Lehmann (Hrsg.): Rechnen und Raten, Köln
1987 (ISBN 3-7614-0930-3)
A.Schmid, I. Weidig: Lambacher Schweizer S8, Mathematisches
Unterrichtswerk, Stuttgart 1995 (ISBN 3-12-730730-6)
A.Schmid, I. Weidig: Lambacher Schweizer S9, Mathematisches
Unterrichtswerk, Stuttgart 1996 (ISBN 3-12-730740-3)
Peter Baptist: Pythagoras und kein Ende? Leipzig, 1998
(ISBN 3-12-720040-4)
Feedback: Email address on my main page
This
page is also available in German.
URL of
my homepage
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |

























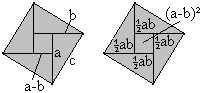




 .........
.........


 ...
... ...
...