|
What is the Hypertetrahedron?
The hypertetrahedron is the four-dimensional tetrahedron.
Other names are simplex or pentatope.
Tetrahedrons
in Perspective
top
The four-dimensional tetrahedron
belongs to the world of thoughts. You can approach it through analogy considerations.
You go from the tetrahedron to the hypertetrahedron. This procedure is
legitimized by the "permanent principle", which is often used in mathematics
to get from the known to the unknown.
. .. |
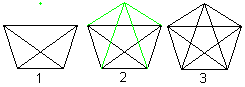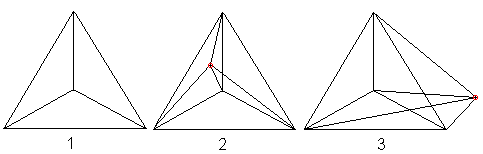
If you connect the corners of a tetrahedron (1) with
a fifth point (2), then you get the perspective view of a hypertetrahedron
(3). |
While a quadrilateral with the two diagonals can be seen
as a perspective view of a tetrahedron, a pentagon with the diagonals represents
a model of the hypertetrahedron.
Characteristics
of the Hypertetrahedron top
The hypertetrahedron has 5 corners (1 tetrahedron and
the fifth point) and 10 edges (1 tetrahedron with 6 edges and 4 connecting
lines to the fifth point).
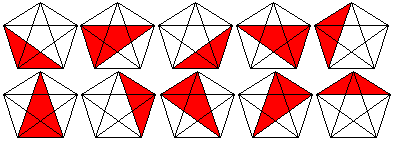The hypertetrahedron has 10 triangles.
The tetrahedron is covered by four triangles. In the same
way five tetrahedrons form the hypertetrahedron.
If you know the 3D-view, you can look at the hypertetrahedron
three-dimensionally, too.
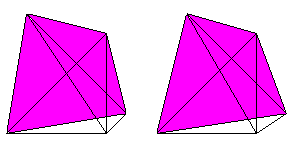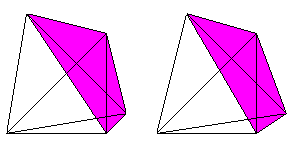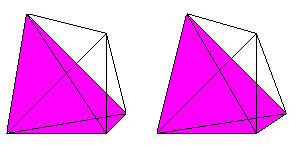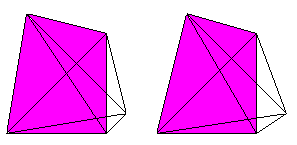4 tetrahedrons, 6 triangles and 4 edges meet at each corner.
3 tetrahedrons and 3 triangles meet at each edge.
2 tetrahedrons meet at each triangle.
Projections
top
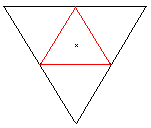
If you give the top view of a tetrahedron (=central projection)
(1) and a fifth point (red) inside (2) or outside (3), you get two models
of the hypertetrahedron. All points must have the same distances from each
other in "reality".
The hypertetrahedron 2 is a triangle with certain lines
inside, the hypertetrahedron 3 a quadrilateral. The model above is a pentagon.
You recognize in all models of the hypertetrahedrons,
that four edges meet at each corner.
Nets top
.. .... |
If you spread out the tetrahedron, you get its net. Together
the four triangles have 4*3=12 sides. 2*3=6 sides (red) are bound. If you
build a tetrahedron, you must stick the remaining 6 sides in pairs. |
 ... |
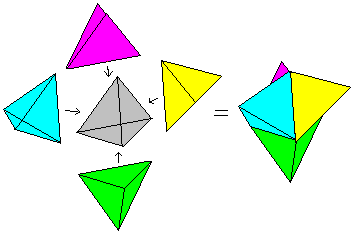If you spread out the hypertetrahedron, you get 5 tetrahedrons
as its net. Together the five tetrahedrons have 5*4=20 triangles.
2*4=8 triangles are bound. If you build a hypertetrahedron, you must stick
the remaining 12 triangles in pairs. |
Formulas top
The considerations above get a
safer foundation by formulas.
"Tetrahedrons" with the dimensions
1, 2 and 3 have the following characteristics.
You would have to determine the data
of the hypertetrahedron in the last line. Dimension=4, corners=5 is clear.
The following law describes how the sequences of the edges and triangles
must be continued.
If you give n=4 into the terms of the
chart, then you get the following data for the hypertetrahedron.
The results for the 5-dimensional tetrahedron
are:
Hypertetrahedron
on the Internet top
German
Marco Möller
Polytope
Wikipedia
Pentachoron
English
Eric W. Weisstein, (MathWorld)
Pentatope,
Simplex
Paul Bourke
HyperSpace,
User Manual
Regular
Polytopes
NN
Pentatope,
Wikipedia
Pentatope,
References
top
(1) Fritz Reinhardt, Heinrich Soeder: dtv-Atlas zur Mathematik
I (Seite 172), München 1977
Feedback: Email address on my main page
This
page is also available in German
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |