|
What is a Polyiamond?
Polyiamonds develop while putting equilateral triangles
together in such way they must have at least one side in common.
The Scottish mathematician T.H. O'Beirne suggested the
name polyiamonds in "New Scientist" 1961 [(1), page 164]. He called the
figures after the diamond.
Simple Polyiamonds
top
 |
You can only form one figure with two or three triangles.
There are three figures of four triangles, the tetriamonds. |
Pentiamonds top
|
There are four figures of five triangles. |
... ... |
If you want to play with them, you should build a set.
Therefore you print a pattern of equilateral triangles,
mark the four figures in a size you like, glue them on cardboard and cut
them out. |
Here is a triangle pattern for
downloading.
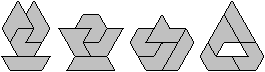
Though the number of pieces is small,
you can design figures:
You can recognize:
1 intercity, 2 sphinx, 3 crooked tower, 4 trapezium without
a corner, 5 terraced houses, 6 motorboat, 7 motorboat with a peephole.
Even symmetric figures are possible:
Hexiamonds top
It is worth working on the pieces with six triangles,
the hexiamonds. You have more pieces than with pentiamonds and therefore
more ways of playing. You can build them in the same way as described above.
There are 12 hexiamonds.
The names of the figures go back to O'Beirne mentioned above.
Playings on Hexiamonds
top
Pentominos are decribed
on another place of my homepage. Pentominos are pieces of five squares.
You can solve different problems like forming rectangles, new figures,
figures with holes, enlarged pentominos or rings. You can transfer these
problems to hexiamonds.
1st Problem: Parallelograms
... ...
|
The Parallelograms 6*12 und 9*8 are possible and solved
on the left. |
2nd Problem:
New
figures
If you design your own figures, you
first must find out, whether you can solve them. You use the chessboard
method: You alternately colour all pieces and count the triangles
of each colour.
If you colour all 12 pieces, then 10 pieces have 3 white
and 3 black (grey) fields, 2 pieces have 4 or 2 black fields. There is
a statement for all pieces: They have the distribution 38+34 or 36+36.
The second sum comes, if you exchange the colours of the two pieces on
the right.
When you have designed a figure and have coloured it like
a chessboard, the distribution of the single pieces must be transfered
to the whole figure.
The following figure has the distribution 38+34. You
can solve it.
It isn't sure that a figure is always possible, if the
distribution is 38+34 or 36+36.
You only can say, maybe it is soluble.
More designs:
Is there a solution? What is it?
3rd Problem: Rings
... ... |
You build a ring of all hexiamonds.
Then you should surround as many connected (white) triangles
as possible.
Is the number 91 the maximum? |
4th Problem: Enclosing
single triangles
... ...
|
You must use all pieces and surround as many single triangles
as possible.
I found eight triangles in a first attempt. |
5th Problem: Small
figures
You needn't use all 12 pieces for building new figures.
|
You form a star of eight hexiamonds or 48 triangles. |
6th Problem: Duplicating
... ...
|
You build a hexiamond with double magnification using
four pieces. Eight pieces are left.
Question: Can you build all hexiamonds like this? |
7th Problem: Tripling
|
You build a hexiamond with triple magnification using
nine pieces. Three pieces are left.
You can only do it with nine hexiamonds (Origin: Instructions
"Verhext") |
8th Problem: Figures
of the same hexiamonds
 |
You can build a larger hexiamond ("Sphinx") with four
equal pieces. |
... ...
|
The small and large hexiamonds needn't be the same.
Example: Four pieces ("yacht") form a larger hexiamond
("rhomboid"). |
The piece "yacht" can cover the whole plane. Question: Which
pieces also tile the plane?
Verhext top
... ... |
There was a famous puzzle with the name "Verhext" (Bewitched)
in Germany in the 1960s. It used all the 12 hexiamonds.
Professor Heinz Haber developped it and presented it
in detail on television and in his magazine "Bild der Wissenschaft".
The pieces had the names Kamm, Kirche, Pfeil, Feile,
Revolver, Haken, Hexagon, Segelboot, Schlange, Tanker, Pfeffermühle,
Dach. |
Manufacturer: Herbert Zimpfer, Metallwarenfabrik, 7586 Altschweier
/ Baden
Puzzle from
different polyiamonds
... |
Name and Manufacturer unknown
Sent by Bodo Schnell
|
Heptiamonds top
There are 24 heptiamonds.
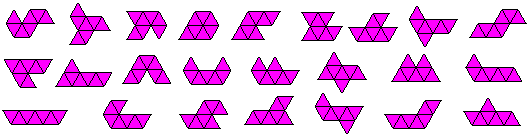Furthermore there are 66 octiamonds, 160 figures of 9 triangles,
448 figures of 10 triangles, and 1186 figures of 11 triangles.
An Email
top
Craig Knecht sent me the following interesting email.
Hi Jurgen Koller,
I have ventured into the world
of polyiamonds. I have made some cartoons and tried to humanize the
subject ...
In the cartoon below -
The fat bird cannot be tiled with
the sphinx tile.
The hexagon with and without the
fat bird can be tiled with the sphinx tile.
I just find that to be interesting
...
I found a proof that all hexagons
can be tiled with the theoretical maximum number of heptiamonds....
https://oeis.org/A298267
https://oeis.org/A291582
Cheers !
Craig
PS https://en.wikipedia.org/wiki/User:Knecht03/sandbox
Polyiamonds
on the Internet top
German
Andrew Clarke (Die Poly-Seiten)
Polyiamonds
Gerd Müller
Hexiamonds
interaktiv
Steffen Mühlhäuser
Rhomba
Thimo Rosenkranz
Hexiamond-Figuren
Wikipedia
Heinz
Haber
English
Andrew Clarke (Die Poly Pages)
Polyiamonds
Col. George Sicherman (Polyform Curiosities)
Mixed
Polyiamond Compatibility
Ed Pegg Jr. (mathpuzzle.com)
iamonds,
octiamonds
and beyond
Eric W. Weisstein (MathWorld)
Polyiamond
Johannes Hindriks
Heptiamonds
N. J. A. Sloane (The On-Line Encyclopedia
of Integer Sequences)
Number of triangular
polyominoes, Number of one-sided
triangular polyominoes
Wikipedia
Polyiamond
References top
(1) Martin Gardner: Mathematisches Labyrinth, Braunschweig
1971 (ISBN 3-528-08402-2)
(2) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (ISBN
3-7701-2097-3)
(3) M.Odier, Y.Roussel: Trioker mathematisch gespielt,
Braunschweig, Wiesbaden 1979 (ISBN 3-5 28-08394-8)
(4) Zusammenlegspiele mit Quadraten und Dreiecken, Bild
der Wissenschaft 11/1965, Seite 946ff., Fortsetzung in Heft 12/1965
(5) Noch einmal: "Verhext", Bild der Wissenschaft 3/1967,
Seite 238ff.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
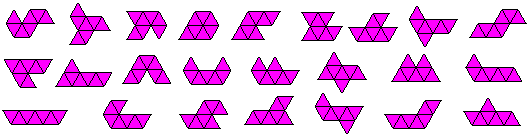
