Ladder Problems
Contents of this Page
What is a Ladder Problem?
Ladder Wall Problem
Ladder Box Problem
Ladder Corner Problem
Crossing Ladders Problem		 Sliding Ladder Problems
Ladder Stories
Ladder Problems on the Internet
References
.
To the Main Page    "Mathematische Basteleien"

What is a Ladder Problem?
A ladder problem is a problem dealing with a ladder.
Two problems are classics, the ladder box problem (drawing) and the crossed ladders problem.
They are special because the problem is simple, but the calculation becomes complicated. 

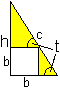
Ladder Wall Problem top
The following problem can be found in a school book in connection to the Pythagorean theorem.
...... 1st Problem:
A ladder c=7m long leans against a wall with the base d=1.4 m from the wall at the base. At which height does the ladder touch the wall? 
Solution: There is c²=h²+d² and hence h=sqrt(c²-d²)=sqrt(7²-1.4²)m=6.9m
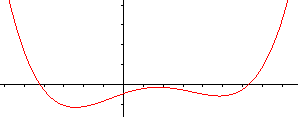
Result: The ladder touches the wall at 6.9m.

When the cosinus function is introduced, you can find the angle of inclination. 
There is cos(alpha)=d/c. Then you get alpha=arc cos (d/c)=arc cos (1.4/7)=78.5°.

Ladder Box Problem top
If you talk about the ladder problem, you usually mean the following problem.
......
 2nd Problem:
A box in cube shape with the edge length 1m stands in front of a wall. A ladder of the length 5m leans against the wall and just touches the box at an edge. How high on the wall is the top of the ladder?

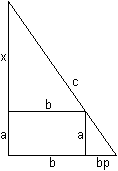
Two solutions
......
 Obviously there are two ways of  leaning a ladder against a wall. 

You often ask for the maximal height so the problem has only one solution. The ladder with the steeper position is meant. This is more real. 
Formula
...... It is not wise to introduce the height at the wall and the distance of the foot of the ladder from the wall as variables. 

The calculation is simpler with x and y because of the symmetry in these variables. 
There are two equations:
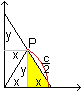
The Pythagorean theorem says (#) c²=(b+x)²+(b+y)². 
There are two similar triangles (yellow) and you have (##) x:b=b:y. 
If you isolate y at (##) and put y at (#), you get c²=(b+x)²+(b+b²/x)² or x4+2bx³+(2b²-c²)x²+2b³x+b4=0.
This is an equation of 4th degree. 
Approximate solution
There is b=1 and c=5. This leads to the equation x4+2x³-23x²+2x+1=0. You find an approximate solution by investigating the graph of the function f(x) = (x4+2x³-23x²+2x+1)/64 and by finding the points at the x-axis. The factor 1/64 is arbitrary and makes a nice graph possible.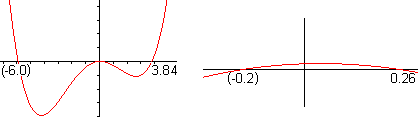
The height of the ladder is 3.84m+1m = 4.84m with x=0.26 and y=1/x=3.84.
Or the height of the ladder is 1.26m with x=3.84 und y=1/x=0.26.
Exact solution
You can use the p-q-formula of the quadratic equation to solve x4+2x³-23x²+2x+1=0.
At first you put c=5 and b=1 and then y=1/x.at the equation (#) c²=(x+b)²+(y+b)².
You get (x+1)²+(y+1)²=25 or (x+1)²+(1/x+1)²=25 or x²+2x+1+1/x²+2/x +1=25 or [x²+2+1/x²]+ [2x+2/x]=25. 
There are z²=x²+2+1/x² and 2z=2x+2/x.with z=x+1/x.
Thus you get the quadratic equation in z:  z²+2z=25=0. The further calculation is:

Result: The ladder reaches the height 4.84m or 1.26m.
Solution with the help of trigonometric formulas sent by Cavan Orwell 
...... The problem described again
There is a ladder of the length c leaning against a vertical wall. It just touching the corner of a b x b square box.
How high does the ladder come up the wall? 
You turn attention to the angle t in this solution. 
Let b=1 and c=5. 
You get 5=1/sin(t)+1/cos(t) because of smilar triangles
and 5=[sin(t)+cos(t)]/[sin(t)cos(t)] oder 5[sin(t)cos(t)]=sin(t)+cos(t).
There is the trigometric identity sin(2t)=2 sin(t)cos(t).
Then there is 2,5sin(2t)=sin(t)+cos(t).
Squaring gives 6,25sin²(2t)=[sin(t)+cos(t)]²=sin²(t)+2sin(t)cos(t)+cos²(t)=2sin(t)cos(t)+1 because of sin²(t)+cos²(t)=1.
This gives 6,25sin²(2t)=sin(2t)+1.
This is a quadratic equation in sin(2t)=y, 6,25y²=y+1 or y²-0,16y-0,16=0.
There are the solutions y1=0,08+sqrt(0,1664) and y2=0,08-sqrt(0,1664).
y=sin(2t) gives 
sin(2t1)=0,08+sqrt(0,1664) or 2t1=29,20° or 2t2=180°-29,2°=150,80°.
The formula h=c*sin(t) gives h1=5*sin(t1)=5*sin(14.60°)=1,26 oder h2=5*sin(t2)=5*sin(75.40°)=4,84.
The solution  y2=0,08-sqrt(0,1664) is negative and leads to angles, which are not possible for the ladder.
Variations
>You can look for integers as solutions of the equation of 4th degree.
>You can replace the cube by a solid.
>You can calculate the ratio how the ladder is divided in two parts. 
...... >You can compress the cube.
Then you can interpret the ladder problem as a triangle calculation.
Give the side c, the angle gamma and the bisector wgamma  in an arbitrary triangle. 
Find the side a.
There is gamma=90° for the ladder problem. 
You find more about this ladder problem at Torsten Sillke's homepage (URL below). 
There you also find the fact that Newton has even worked on the problem "segment in a corner".

Kent Holing (2) has raised the question when and where the problem "Single Ladder Problem" turned up for the first time. 
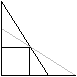
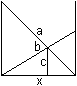
"The oldest reference to the square box problem we know is from 1754. (Thomas Simpson: A Treatise of Algebra, John Nourse, Lomndon 1745, page 250). For the general box problem the oldest reference we know is from 1907. (A.Cyril Pearson: The Twentieth Century Standard Puzzle Book, George Routledge&Sons, Ltd., London 1907, page 103.)"

Ladder Corner Problem top
...... 3rd Problem:
There is a ladder with the length c and a corridor with the width b. Unfortunately the corridor has a right angled bend. How long may a ladder be so that it can be moved around the corner?
This is a maximum problem. The length of the ladder c (or c² for calculation reasons) shall have the maximum value.
......
 The Pythagorean theorem leads to (#) c²=(x+b)²+(y+b)².
There is (##) ist y:b=b:x or y=b²/x because of the similar yellow triangles. . 
If you replace y at (#), you get the function c²=(x+b)²+(b²/x+b)² or c²=x²+2bx+b4/x²+2b³/x+2b².
The first derivative is (c²)'=2x+2b-2b4/x³-2b³/x². (The second derivative is positive for x>0) 
(c²)'=0 leads to the equation of 4th degree x4+bx³-b³x-b4=0. You easily find out that x=b is a solution. 
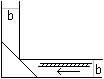
x=b leads to c/2=sqrt(b) or c=2sqrt(2)b. This solution is illustrated in the drawing above. 
Result: The ladder with the length c=2sqrt(2)b is the longest one.

A more general solution - sent by Johan Asma
It is convenient to introduce the varialbe p, so that b+pb=(1+p)b is the horizontal line segment. 
Then there is x:(a+x)=b:[(1+p)b] or x=a/p.

The Pythagoras theorem gives c²=(a+a/p)²+(b+pb)² or c²=a²(1+1/p)²+b²(1+p)²
or c²=a²(1+2/p+1/p²)+b²(1+2p+p²).

You look for the value of p so that c=c(p) is a minimum. 
You need the first derivate c' or simpler (c²)'=a²(-2/p²-2/p³)+b²(2+2p).
(c²)'=0 gives a²(-2/p²-2/p³)+b²(2+2p)=0 or a²(-2p-2)+b²(2p³+2p4) or -2a²(p+1)+2b²p³(1+p) or (-2a²+2p³b²)(p+1)=0. 
The solution is p³=a²/b² or p=(a/b)2/3.

Let b=a. Then p=1 and c²=a²(1+2/p+1/p²)+b²(1+2p+p²)=b²(1+2+1)+b²(1+2+1)=8b² or c=2sqrt(2)b.

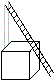
You can also give the problem as a ladder box problem:
A box in cube shape with the edge length 1m stands in front of a wall. A ladder leans against the wall and just touches the box at an edge. How long is the shortest ladder?
Hans-Joachim Simon sent me the following solution.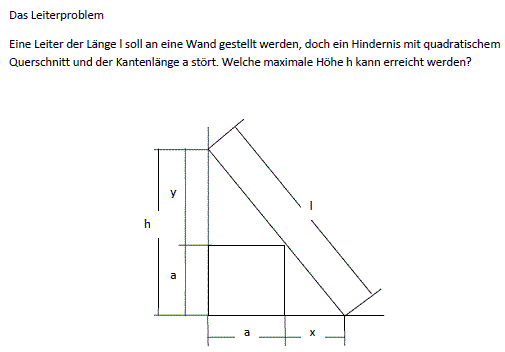




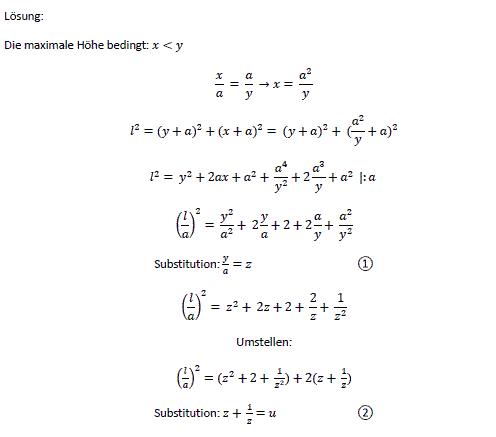
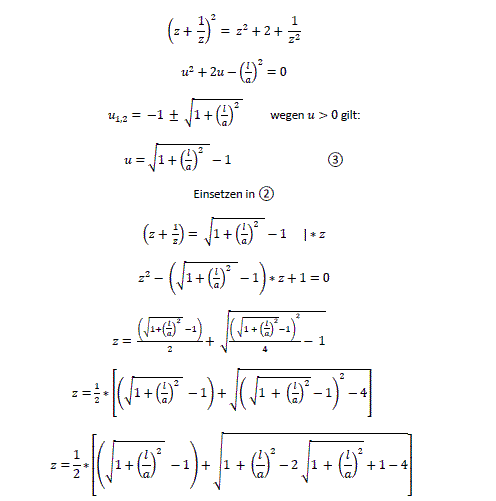
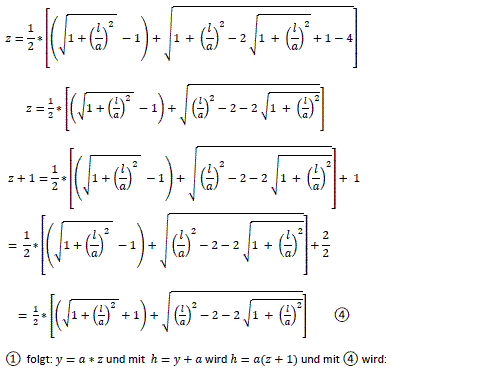
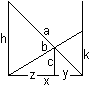
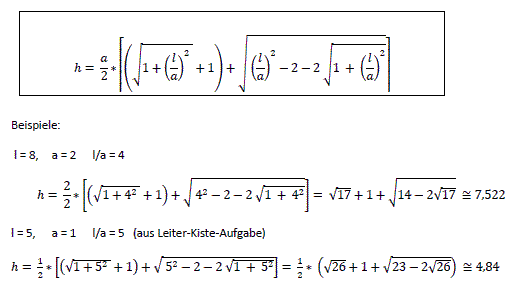Crossing Ladders Problem top
Martin Gardner (1) published the following problem and it became popular. Starting the solution is easy, but then it becomes as difficult as the ladder box problem.
...... 4th Problem:
There are two ladders between two houses. 
How long is the distance x between the house walls if the lengths of the ladders a and b and the height c over the ground of the crossing  are given?

Attempt of a solution
You introduce the four variables h, k, y, and z (drawing)

There is (#) y:c=x:h and z:c=x:k because of similar triangles.
The product equations are yh=cx and zk=cx.
The Pythagorean theorem leads to (##) a²=x²+h² and b²=x²+k².
Then there is (###) x=y+z
Isolate h and k at (##) and replace them at first at (#) and then at (###). You get:
If you want to remove the roots you must square the equations twice. 
Then you get an equation of 8th degree :-(.
Solution as replacement
You don't calculate the distance of the wall directly but via the height h of the longer ladder.

You get 1=c/h+c/k and k=ch/(h-c) with (#) and (##).
(##) gives a²-h²=b²-k². 
If you replace k=ch/(h-c) at a²-h²=b²-k², you get h4-2ch3-(a²-b²)h²+2c(a²-b²)h-c²(a²-b²)=0  after some steps.

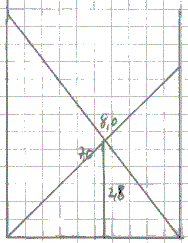
Example with numbers 
...... You draw  the ladders a=8.0 and b=7.0 between two walls of the width x=5. Then there is c=2.8.
The unit may be 1m suitable for ladders. 

Then the equation of 4th degree is 

h4-5,6h3-15h²+84h-117,6=0.
A function belonging to it is 
f(h)=(h4-5,6h3-15h²+84h-117,6)/256.
The graph has h=0 to f(x)=0. Then the Pythagorean theorem leads to x=4,9.		 ......
Result: Drawing and calculation lead to about the same results.

The attraction of the problem in recreational mathematics is not in finding the distance of house walls. It is a challenge to find integers as values and the integers as small as possible for the different lengths. 
You find a collection in Gardner's book. 
Kent Holing (2) has raised the question when and where the problem "Crossed Ladders Problem" (CLP) turned up for the first time. 
"The oldest reference to the CLP we know is from 1894. (Problem 24. The American Mathematical Monthly, 1 (1894), 353-354)"

Sliding Ladder Problems top
...... A ladder only stands if there is friction between the top of the ladder and the wall and - more important - between the foot of the ladder and the ground. 

5th problem:
Find the curve which the centre of the ladder draws during sliding!
......
 Assume P(x|y) is a curve point and c the length of the ladder. 
y=c/2, if x=0. - x=c/2, if y=0.
There is the Pythagorean theorem  x²+y²=(c/2)². 
This is the equation of a circle. 
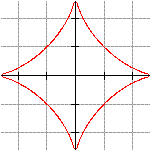
Result: The centre of the ladder is moving along a circle.
Generalization: Which curve draws an arbitrary but fixed point of a ladder during sliding?
Astroid
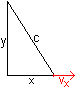
...... If you draw all positions of a sliding ladder you get an astroid as an envelope (on the left).

You see the complete astroid with |x|^(2/3)+|y|^(2/3)=c^(2/3) and c=2 on the right.

 ......
6th Problem:
A ladder c=5m long is leaning against a wall. The foot of the ladder is pulled away from the wall at a speed of  vx =0,3m/s just when it is x=3m from the wall. How fast is the top of the ladder moving down the wall?
General solution
...... Assume c is the length of the ladder.
Assume x(t) and y(t) are the distances of the ends of the ladder from the corner wall/ground. 
The dependence on the time is given by the tag (t).
vx =x'(t) and vy =y'(t) are the speeds.
There is [x(t)]²+[y(t)]²=c².
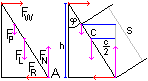
The derivation is 2x[x'(t)] +2y[y'(t)]=0, hence is y'(t)=-{x[x'(t)]}/y(t)} = -{x[x'(t)]}/sqrt{c²-[x(t)]²}=vy.
Solution with numbers
Let c=5m, x=3m and vx =0,3m/s:
vy=-3*0,3/sqrt(5²-3²)m/s=-0,23m/s
Result: The top of the ladder is moving downwards with a speed of 0,23 m/s.
7th Problem: 
A uniform ladder of the length l=5m and the mass m=30kg leans against a wall at an angle of phi=30° to the wall. A man of the mass M=60kg ascends up the ladder. How far can he climb before the ladder slips? The coefficient of friction between the foot of the ladder and the ground is f=1/3. Assume there is no friction along the wall.
Solution:

Forces
...... There are the weights of the man (FP=Mg) and the ladder (FL=mg).
FN und FW are the normal reactions at the ground and at the wall. 
The ladder is held by the frictional force FR at the ground.

Equilibrium of forces: FW=FR and FN=FP+FL.
Equilibrium of moments about A:  (#) FW*c cos(phi)=FP*s sin(phi)+FL*(c/2)*sin(phi)
Further calculation:
The ladder is about to slip just when FR=f FN is. Hence you replace FW  in (#) by f(FP+FL):
f (FP+FL)*c cos(phi)=FP*s sin(phi)+FL*(c/2)*sin(phi)
Replace the forces by the masses with FP=Mg and  FL=mg: 
f(M+m)*c cos(phi)=M*s sin(phi)+m*(c/2)*sin(phi) or 
(##)   cf(M+m)=Ms tan(phi)+m(c/2)tan(phi) 
Isolate s: 
Solution with numbers:
Let c=5m, f=1/3, m=30kg, M=60kg and phi=30° , then s=3.1m.
Result: The man can ascend 3.1m.
The solution of the next problem is a special case in the latter calculation.
8th Problem:
A uniform ladder of the length c=5m and the mass m=30kg  leans against a wall. Assume there is no friction along the wall. The coefficient of friction between the foot of the ladder and the ground is f=1/3.
At which angle starts the ladder to slide?
Solution:
Put M=0 in (##) and you get  fmc=m(c/2)tan(phi). Hence there is f=(1/2)tan(phi) or phi=arc tan(2f).
Solution with numbers: phi =arc tan(2/3)=33.7°. 
Result: The angle between the ladder and the wall is just 33.7°.

Ladder Stories    top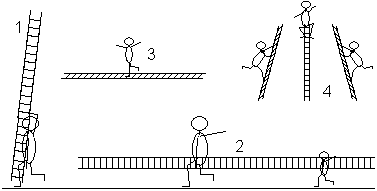

1 Father is carrying a ladder. 
2 Father and son are carrying a ladder. 
3 A child is balancing on a ladder.
4 An circus acrobat is ascending a ladder and descending on the other side. Maybe he performs a handstand at the top or he walks with the ladder.

You can physically explain the issues considering moments.

Ladder Problems on the Internet     top

German

Bernd R. Mentjes
Das Leiterproblem  (Leiter-Kiste-Aufgabe)

Hans-Jürgen Caspar (bei Mathroids Matheplanet))
Die Leiter und die Sternkurve    (Die Astroide heißt auch Sternkurve) 

Mathematischer Korrespondenzzirkel (Universität Göttingen)
Aufgabe 2   (Leiter-Kiste-Aufgabe)

Matroids Matheplanet Forum Index
Malerarbeit mit Hindernissen
Aufgabe: Malermeister Patzmann hat ein Problem. Er soll einen Saal ausmalen und muss dazu erst eine (möglichst lange) Leiter durch die Kellergänge transportieren. Die Gänge sind rechtwinklig verzweigt und haben quadratischen Querschnitt, 3m breit und 3m hoch. 

René Grothmann
Der Stab, der um die Ecke muss, und einhüllende Kurven

Wikipedia
Tragbare Leiter

English

Philip Spencer
Classic Fallacies: A Ladder Will Fall Infinitely Fast when Pulled

Eric W. Weisstein (MathWorld)
Crossed Ladders Problem,  Crossed Ladders Theorem,  Moving Ladder Problem

Frank Wolfs
Sample Problem 13-3 (Ladder and Friction)

Jim Wilson
Ladder and Box Problem,  Help with equations

Marek Szapiel (Lawrence S. Husch, visual calculus)
Shortest Ladder over a Fence,  The Longest Ladder

Torsten Sillke
Ladder-Box Problem,  Ladder- move a ladder around a corner,  Hinged Ladder - distance problem

Wikipedia
Crossed ladders problem

References   top
(1) Martin Gardner: Mathematischer Zirkus, Ullstein Berlin Frankfurt Wien 1988 [USBN 3 550 07692 4]
(2) Kent Holing (Statoil Research Center, Trondheim, Norway): Ladder Problems Revisited (privater Zugang)
(3) Duncan Graham u.a.:A Level Mathematics, Letts Editional London 1995 [ISBN 1 85758 338 8]

Gail from Oregon Coast thank you for supporting me in my English.
Feedback: Email address on my main page

This page is also available in German.

URL of my Homepage:
https://www.mathematische-basteleien.de/

©  2004 Jürgen Köller

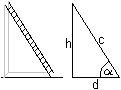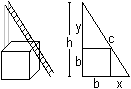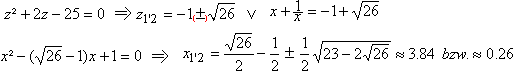
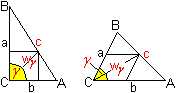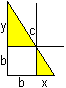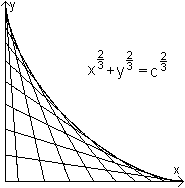top