|
MacMahon's Coloured Cubes
|
What are MacMahon's Coloured Cubes?
MacMahon's cubes are the cubes which develop if you give
the six sides six different colours in all possible combinations.
... ... |
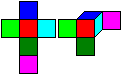The colours are not determined. You can choose any colour.
I chose red(1), light blue(2), dark blue(3), dark green(4), light green(5),
and pink(6).
A cube is drawn on the left as a net and in perspective
with three turned square sides. |
P.A.MacMahon was an English mathematician and major. He lived
from 1854 to 1929.
There are
30 MacMahon Cubes top
... ... |
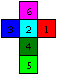If you give the squares of a cube the numbers 1, 2, 3,
4, 5, 6 and form all permutations of the six numbers, you get 1*2*3*4*5*6=6!=720
cubes.
Many among the cubes are the same. They can be transferred
by turns around one of the 13 axles into one another. There are 24 turns
and thus only 720:24 = 30 different cubes. |
The following picture illustrates these facts. The numbers
below the cubes mean the number of the turns.
Making of the Cubes
top
You also get the 30 cubes by systematic colouring.
.... .. |
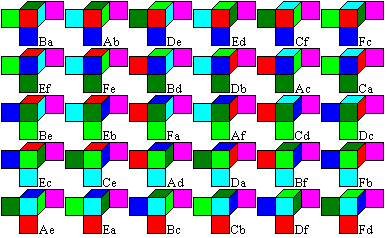> All cubes get the colour pink on the reverse side.
> The front sides get one of the six colours in each line.
> The sides underneath get the third suitable colour in
each line .
> The remaining three sides get all permutations of the
remaining three colours in a line.
The names like Ba or Fa come from J.H.Conway (see
below). |
If you want to play with the coloured
cubes, you must build them yourselves.
... ... |
You can write the numbers 1 to 30 (in place of the colours)
on round self-adhesive labels and stick them on the cubes. Each cube should
get a name like Ab in order to keep track of things.
It is more beautiful, of course, if you use larger cubes
and give them the six colours. |
Figures with Cubes
top
Playing with the cubes is looking
for right rectangular solids or big cubes with one-coloured sides.
The following four figures are
relatively easy to find.
The cube on the left is extended twice
by a 1x2x2-slice to the left. 3x2x2 and 4x2x2-solids develop.
The small cube on the left is used
for forming the corners of the large cube on the right. You can easily
find the 19 remaining cubes.
... ... |
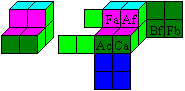The L-shaped figure on the left
is built by symmetrically coloured cubes (see below).
The speciality is that inside the
same colours touch as additional condition. This is the so-called domino
condition (Gardner). |
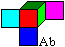
MacMahon's Problem
top
The main problem is MacMahon's
problem.
... ...
|
You select a cube from the 30 cubes,
e.g. the cube Ab. |
 ... |
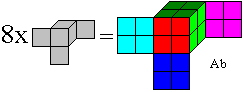29 cubes remain. You select eight
among them to build a 2x2x2 cube with the same colours as the small cube.
The same colours must touch inside, too, to make the puzzle more difficult. |
A description of the way to the solution for the cube Ab
follows.
You can't find the solution by accident. You must proceed
systematically.
First you look for the four cubes in the lower layer.
Lay all cubes with dark blue underneath.
The cubes Bc, Ca, Df, Ed, and Fe are possible for the
cube at the bottom, on the left, in front. Take out Df, Ed, and
Fe, because inside and outside would be the same colour. Bc and Ca
are left. (Lay Bc aside. This would lead to a second solution.)
The cubes Bd, Cf, Da, Ec, and Fe are possible for the
cube at the bottom, on the right, in front. Bd is left.
The cubes Bd, Cf, Da, Ec, and Fe are possible for the
cube at the bottom, on the left, in the back. Bf is left.
The cube Ea is only possible for the cube at
the bottom, on the right, in the back.
Turn the remaining cubes so that dark green is at the
top.
The cubes Be and Cd are possible for the cube at the
top, on the left, in the front. Be is left.
The cube Fa is only possible for the cube at
the top, on the right, in the front.
The cube Da is only possible for the cube at
the top, on the left, in the back.
The cube Bc is only possible for the cube at
the top, on the right, in the back.
Hence the solution is:
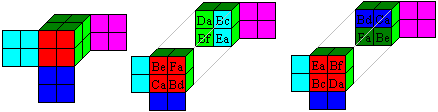There is the second solution on the far right, which I mentioned
while looking for the solution. You use the same cubes. They lay symmetrically
to the centre and are turned.
J.H.Conway takes the credit
for a complete solution of the problem.
...... ... |
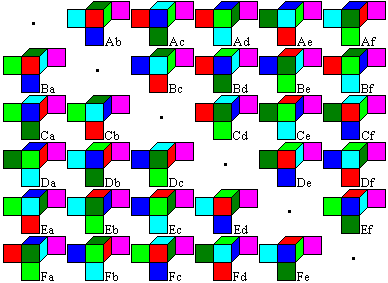He arranged the 30 cubes in a 6x6-field,
whereby he kept the main diagonal free.
The columns are called a, b, c,
d, e, f,
the lines A, B, C, D, E, F.
Thus each cube gets a pair of a
large and a small letter as a name depending on its position. |
The speciality of the table is that
it contains all solutions of MacMahon's problem for all cubes.
If you want to build i.e. the cube
Ab as a 2x2x2-cube, you can easily find the eight cubes:
You go from Ab to the mirror cube
Ba and choose the remaining eight cubes in the line and the column with
cube Ba.
... ... |
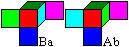Cube and mirror cube have mirror
images, for instance Ab and Ba. |
Still another feature:
... .... |
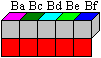If you choose the five cubes of
a line or of a column and build a 1x1x5-bar and make sure that any colour
lies down, the remaining five colours lie above. |
The Mayblox Problem
top
Eight cubes are given. Form a 2x2x2
cube with six colours at every side and the same colours touching inside.
You have no small cube as a model. This is an additional difficulty.
Kowalewski's Problem
top
The German mathematician G. Kowalewski
varied the 8-cube-problem.
... ... |
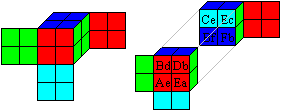It required the same colours on
the right and on the left and in front and on the reverse side. A third
and a fourth colour are at the top and underneath. Inside equal colours
should meet.
This problem has only two solutions. One solution is shown.
You need eight more cubes for the second solution. |
Instant Insanity
top
"Parker Brothers" introduced the
"color matching box" with the name "Instant Insanity" in the year 1967.
The puzzle was called "Vier verrückt" or "Katzenjammer-Puzzle"
in Germany. Twelve millions were sold world wide
(!?).
... ... |
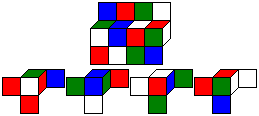This puzzle has four coloured cubes.
In contrast to Mac Mahon's cubes only four different colours are used.
The problem is to arrange the cubes
to a 1x1x4-bar, so that four different colours appear on all four sides.
Here is one solution. |
... ... |
It is also possible to build a
bar from Mac Mahon's cubes, so that six different colours appear on all
four sides. In addition the same colours touch inside. Even the ends of
the bars have the same colour.
There is one solution on the left.
The colours lie diagonally. |
... ... |
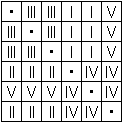You can divide the 30 cubes into five groups with six
cubes each, so that you can form five bars just described [
Zoltan Perjés, book 6].
You can assemble them in the Conway scheme and name them
with Roman letters. The drawn bar has the number I.
The speciality is, that the cubes lay together and that
you can partly assemble them not only side by side, but also before one
another or underneath the other without changing their properties of the
different coulors in one row and the domino condition
(noticed by Torsten Sillke). |
Coloured
Cubes on the Internet top
German
Wikipedia
Percy
Alexander MacMahon
English
Jaap Scherpius (Jaap's Puzzle
Page)
Octacube,
Instant
Insanity
John J. O'Connor & Edmund F.
Robertson, University of St Andrews
Percy
Alexander MacMahon
Kadon Enterprises Inc.
Frank
Armbruster invented Instant Insanity
Torsten Sillke
MacMahon's
cubes (Multiple Cubes, Probabilities,
References)
Wikipedia
Percy
MacMahon, Instant
Insanity, MacMahon
Squares
French
Charles-É. Jean
(Dictionnaire de mathématiques récréatives)
Cube
coloré
References top
(1) Gerhard Kowalewski: Alte und neue mathematische Spiele,
Leipzig 1930 (Reprint bei Teubner, Stuttgart 1978)
(2) Bruno Kerst: Mathematische Spiele, Berlin 1933 (Nachdruck:
Martin Sändig, Wiesbaden 1968)
(3) Gardner, Martin: Mathematische Knobeleien, Braunschweig
1980 (Vieweg)
(4) Rüdiger Thiele: Das große Spielvergnügen,
Leipzig 1984 (Urania-Verlag)
(5) Gardner, Martin: Mathematische Hexereien, Berlin
1988 (Ullstein)
(6) Gardner, Martin: Fractal Music, Hypercards
and More Math. Recreations from SA Magazin, New York 1991 (Freeman)
(7) Rüdiger Thiele, Konrad Haase: Der verzauberte
Raum, Leipzig/Jena/Berlin 1991 (Urania-Verlag)
(8) Rüdiger Thiele, Konrad Haase: Teufelsspiele,
Leipzig/Jena/Berlin 1991 (Urania-Verlag)
Thanks to Sabine Sprankel for the idea of this topic
and Torsten Sillke for supporting me.
Thanks to Gail from Oregon for supporting me in my translation.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |