|
What are Polyhexes?
Polyhexes are figures which you can form with at least
two hexagons.
You order and call them by the number of the hexagons.
| You can build one figure by two
hexagons and three trihexes by three hexagons. |
... ...
|
| There are seven tetrahexes. |
 ... |
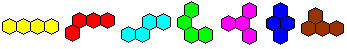Furthermore there are 22 pentahexes. Computers found 82 hexahexes,
333 heptahexes, 1448 octahexes or 8-hexes, 6572 9-hexes, 30490 10-hexes,
143552 11-hexes, 683101 12-hexes, ... (Book 2, page 152 and 160).
Martin Gardner described polyhexes
in the magazine Scientific American and made them popular. He repeated
that in book 2 (Page 149ff.) and added readers' results.
Making of Tetrahexes
top
If you want to play with polyhexes, you must build them
yourself.
There are several methods.
1st method:
Print a picture with equilateral triangles (6 triangles=1
hexagon), mark the seven pieces, glue them on cardboard and cut them out.
Here is a drawing of equilateral
triangles for downloading.
2nd method:
The densest sphere packing in the plane corresponds with
a hexagon pattern. Glue balls to each other so that you get tetrahexes.
3rd method:
It is said that you can also glue nuts (which belong
to screws) together.
You could buy a set of tetrahexes.
... ... |
The firm Kipfer CH-3303 Jegensdorf offered the
set on the left with the name HEXAGON.
It is described in the packing as follows:
"Puzzle containing 7 parts: You can create more than 900
symmetrical shapes! 92 examples and solutions on coloured cards are enclosed." |
You also could find a set of tetrahexes in the catalogue
of the Swiss firm Naef. It is shown on the Japanese web site below.
Playing with
Tetrahexes top
Here are the seven tetrahexes once again. The names under
the pictures are from book 2.
........
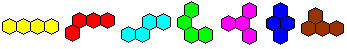bar, worm, wave, arch, propeller, bee, pistol
I suggest to replace the name pistol by locomotive.
There are several questions according
to the pentominos, the figures with five squares.
Parallelogram
Seven tetrahexes have 28 hexagons altogether. The question
is whether there is a parallelogram 4x7.
There is one....and more:
Source: book 3, page 125
Triangle
... ... |
28 is a triangular number. That is 28=1+2+3+4+5+6+7.
Thus you can form a triangle of 28 hexagons (on the left).
You can't solve the figures with tetrahexes (Torsten Sillke, URL below).
You must be content with an "alternate triangle" (on the
right). |
... ... |
Figures of
Tetrahexes
It is not easy to lay figures. Best is to keep it up
and wait and see. You must not use all pieces. Symmetric figures are always
nice.
You better recognize the shapes if you only use one colour.
Figures of
all Tetrahexes
My bird, my boat, my...
You can solve the following figures.
Source: Book 2, page 151
Ring
There is the problem of forming
a ring including as many hexagons as possible.
34 hexagons are included.
|
35 hexagons are possible. (Source: Livio Zucca, URL below).
|
This is a nice aspect of mathematics:
Better solutions lead to more handsome figures.
Are there more than 35 hexagons?
Figures with
as many holes as possible
|
Can you break the number 6? |
Tiling the
Plane
... ... |
You can fill the plane with only one tetrahex. The propeller
is one example. You form a figure with four propellers, which repeat in
the plane.
(Steven Dutch, URL below). |
Tiling a Triangle
... ... |
As mentioned above you can't lay the triangle on the
left with all tetrahexes. It is possible to choose one, the locomotive.
This is the only piece which, itself, can fill the triangle.
(Book 3, page 124) |
Tetrahexes, expanded
top
It is useful not to adhere at seven tetrahexes, but to
widen the set. The ways of playing are larger and the puzzles simpler.
You can reflect the asymmetrical pieces, so that you get
10 pieces with 40 hexagons. They are called "one-sided polyhexes". You
find rectangles 5x8 and 4x10 on Andrew Clarke's web site (URL below).
You get 12 pieces and 40 hexagons
if you add pieces with one, two and three hexagons.
You find a ring formed by all pieces on Kate Jones's web
site (URL below).
Pentahexes top
22 Pentahexes:
The number is too large to give an interesting puzzle. Pentahexes
is a topic more for computers. Many people have worked on these pieces,
as you can see in book 2 and several web sites. I restrict myself on a
parallelogram 10x11 on this page. The puzzle pieces of the series "Beat
the Computer" from the 1970s are packed in this shape.
Polyhexes on
the Internet
top
German
Andrew Clarke (The Poly Pages)
Polyhexen
Peter F.Esser
Puzzle
aus Muttern
Thimo Rosenkranz
Tetrahex-Figuren
Torsten Sillke
Triangles
and Pyramids with equal Polyspheres
English
Andrew Clarke (The Poly Pages)
Polyhexes
Eric W. Weisstein (World of Mathematics)
Polyhex
Erich Friedman (Math Magic)
Triangle
tilings
Joseph Myers
Polyomino
tiling
Kate Jones (Kadon Gamepuzzles)
A
New Puzzle Genre: Polyforms
Miroslav Vicher
Polyhexes
Peter F. Esser
Front
and Back Colored Tetrahexes
Steven Dutch (Professor Dutch's home page)
Polypolygon
Tilings
Torsten Sillke
The
Impossible Tetrahex Triangle
Wikipedia
Polyhex
(mathematics)
Dutch
NN
Polyhexes
References top
(1) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont
taschenbuch1480) [ISBN 3-7701-2097-3]
(2) Martin Gardner: Mathematischer Zirkus, Berlin 1988
(ISBN 3550076924)
(3) Solomon W.Golomb: Polyominoes, Princeton, New Jersey
1994 (ISBN0-691-08573-0)
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
