What is the Happy Cube?
... ...
|
The puzzle Happy Cube consists
of 6 mats of foam coloured blue, green, yellow, orange, red, and
violet. Here you can see the blue mat.
Each mat has six 5x5 pieces surrounded by a frame. Small
cubes are cut irregularly along the edges. It is possible to put the six
5x5 pieces together to a 5x5x5 cube, if you find special positions. |
... ... |
For each colour there are various levels of difficulty
of solving. The blue mat is easy to solve, the purple one is the most difficult.
The Happy Cube was designed by Dirk Laureyssens in 1986.
It received several names such as the I.Q.ube, de Wirrel Warrel Kubus,
CocoCrash and Cube-it.
Dirk Laureyssens' variants are:
The Little Genius, the Profi Cube, the Marble Cube
(work
together with Happy Cube)
Further there are the Planet Cube, Snafu, Snuzzle,
and Crico. |
Notation of a
Solution top
...
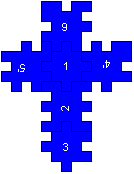4'/5'16/2/3
|
You can number the six pieces from 1 to 6 on the front
side. You can recognize the front side by a little circle in one corner
on the left (blue: left up). You name the rear side of 1 1', corresponding
2' to 6'. If you find a solution, you form a base of the cube, which
is a cross. Make sure that 1 is upright in the middle. Then the description
is definite.
You also number the other mats for the solutions. Notice
the little circle on the left showing the front side. |
Figures (Simple Cubes below)
top
Box 1x1x2
... ...
|
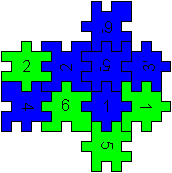You can put together a figure of two cubes with the help
of the blue and green mats.
You take 10 pieces of 12.
2 pieces are left. |
Box
1x1x3
... ...
|
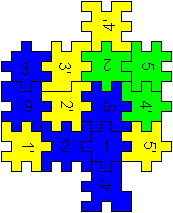You can put together a figure of three cubes with the
help of the blue, green and yellow mats.
You take 14 pieces of 18.
4 pieces are left. |
Box
2x1x2
... ...
|
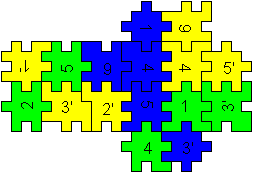You can put together a figure of four cubes with the
help of the blue, green and yellow mats.
You take 16 pieces of 18.
2 pieces are left. |
Maxi-Cube
2x2x2
... ...
|
You can put together a figure of 2x2x2-cube with the
help of all the 6 mats. You take 24 pieces of 36. 12 pieces are left.
Theoretically you can build it with 5 mats.
If you use 4 mats, you get 24 pieces. That is sufficient.
But you can show, that you need 26 cubes for all the corners, but 4 mats
only have 6*4=24 corner cubes.
So it is not possible to form a maxi-cube with 4 mats.
|
Maxi-Cube
2x2x2
... ...
|
There is even a solution, which has the same colour on
each side.
(Jan Verbakel, Eindhoven, 1, Seite 15) |
3D
Cross
... ... |
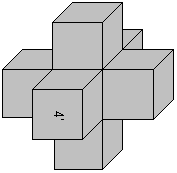If you want to build the figure on the left, first you
have to put five pieces together to form four open cubes. The middle piece
is at the bottom. (You have to keep the orientation in the space.) Then
you form a ring of the four open cubes.
At last you form two open cubes by the pieces on the
very right and put them at the bottom and at the top of the ring. |
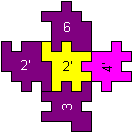
on the left
|
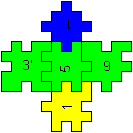
at the back
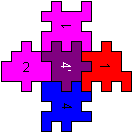
in front
|
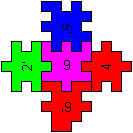
on the right
|
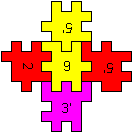
at the top
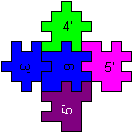
at the bottom
|
You take 30 pieces of 36. Six pieces are left.
1x2x3-box with
a collar
It is nice to include the frame. Here is a solution by
Jan Verbakel (1, page 21):
Rectangles top
Jean-Marc Dubrunfaut was looking for a rectangle formed
by all 36 mats in order to use a laser cutter.
.... .. |
He found this 18x2 square. |
There is 36= 36x1 = 18x2
= 12x3 = 9x4 =6x6 and so perhaps there are
five rectangles.
Some Mathematics top
Every piece has 4 edges. If you turn a piece, you have
4 more edges. You write down a pattern of an edge with a sequence of
0 and 1. This is a number with 5 digits in the binary system. If there
is no little square, you write 0. If there is a little square, write 1.
This method will be shown by piece number 4. In the drawing the number
is related to the edge near to the number.
|
In this way you can fix the number of the 6x6x4x2 = 288 patterns
of the edges for all the mats in a chart.
decimal
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
number of the patterns: |
binary
00000
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
10001
10010
10011
10100
10101
10110
10111
11000
11001
11010
11011
11100
11101
11110
11111
. |
blue
-
-
-
-
16
2
-
-
-
-
10
4
-
-
-
-
-
-
-
-
2
4
-
-
-
-
4
6
-
-
-
-
8 |
green
-
-
-
-
14
4
-
-
-
-
10
4
-
-
-
-
-
-
-
-
4
2
-
-
-
-
4
6
-
-
-
-
8 |
yellow
-
-
-
1
8
6
-
1
-
-
12
4
-
-
-
-
-
-
-
-
6
2
-
-
1
-
4
2
1
-
-
-
12 |
orange
-
-
1
1
10
1
3
-
1
1
6
5
3
-
-
-
-
-
1
-
1
6
-
-
1
-
5
2
-
-
-
-
16 |
red
-
-
1
1
10
3
2
-
1
-
8
3
2
1
-
-
-
-
-
1
3
2
1
-
1
1
3
4
-
-
-
-
18 |
purple
-
-
2
3
6
4
1
3
2
-
6
3
1
1
-
-
-
-
-
-
4
-
1
-
3
-
3
2
3
-
-
-
17 |
sum
-
-
4
6
64
20
6
4
4
1
52
23
6
2
-
-
-
-
1
1
20
16
2
-
6
1
23
22
4
-
-
-
. |
You can see:
> Only 22 of 32 possibilities are used to form an edge
(black letters).
> All the pieces with x000x or x111x are avoided (red
letters).
> The four pairs (00100,11011), (00101,11010),
(01010,10101) and (01011,10100) going together appear frequently (240 of
288). They occur at every colour with one exception. They are used
exclusively at blue and green (bold letters)
> Patterns like x11xx, xx11x, x00xx or xx00x do not occur
at blue and green.
> Two pairs are the same, red4/blue3 und orange4/violett4.
Symmetries top
You find a cube easier, if there is symmetry.
.
Symmetric edges:
Symmetric pieces with two axes
Symmetric pieces with one axis |
blue
36
2
1 |
green
32
1
2 |
yellow
24
0
0 |
orange
24
0
2 |
red
24
0
1 |
violet
14
0
0 |
Cube Solutions top
The main problem is making a cube with one colour. Students
found all solutions by trying. I give only one drawing for one colour.
Symmetric solutions are counted once.
One of three solutions
4'/5'16/2/3
|
One of five solutions
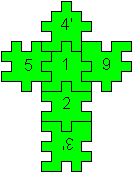
4'/516/2/3'
|
One of five solutions
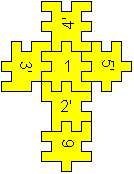
4'/3'15'/2'/6
|
The only solution [orange ;-)]
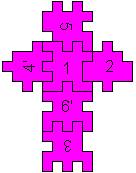
5/4'12/6'/3
|
.The only solution
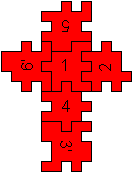
5/6'12/4/3'
|
.The only solution
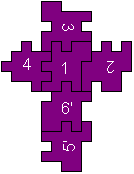
3/412/6'/5'
|
The blue and the green cube can be easily done. The blue
cube is more difficult, because the pieces 1, 2 and 3 must follow in the
same sequence for every solution.
I would give the yellow cube the lowest degree of difficulty.
The edges 00011 (piece 2) and 11100 (piece 3) fit together, piece 1' complete
them to a half cube. Then it is not far away to the whole cube.
It is very difficult to solve the purple cube, because
you are often on the wrong track.
All solutions:
blue, 3 solutions: 4'/5'16/2/3,
2/4'15/6'/3', 4'/612/5'/3
green, 5 solutions:
4'/516/2/3', 6/213/4/5, 2/6'13/4/5, 3/415/6'/2, 3'/514'/2/6'
yellow, 4 (5) solutions:
4'/3'15'/2'/6,
6/3'15/2'/4', (6/3'15'/2'/4',) 6/4'12'/5'/3', 4'/612'/5/3'
orange, 1 solution:
5/4'12/6'/3
red, 1 solution: 5/6'12/4/3'
violet, 1 solution: 3/412/6'/5'
... ... |
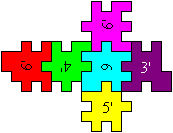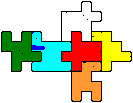
You can also form a mini cube of six pieces with different
colours.
There are computer results about forming a mini cube with
different colours in article 1 (11pp):
19 mini cubes with the distribution 3+3 (2 colours),
88 with 2+2+2 (3 colours), 21 with 1+1+1+1+1+1 (6 colours). |
... ... |
Benjamin Koch even found 41 solutions with six different
colours instead of 21 with help of his computer. |
Snafooz top
Snafooz is an American copy with six models. It goes
into competition with the Happy Cube family.
... ...
|
Snafooz is common in the USA.
There are also six mats. A 6x6-square forms the side of
a cube, not a 5x5-squares like at Happy Cube.
(Drawing by Xandur, USA)
|
Rubber top
... ... |
There is a puzzle from Japan, which
uses a 4x4-square as a basis. The six pieces, which form a cube, show animals
because of shape and decoration. The material is known from the rubber.
That is what the pieces should be.
My puzzle has only Japanese letters.
In the article (1) you find, that
you can read SEED, PLASTIC ERASER, MADE IN JAPAN on the plastic box:. |
References top
(1) Jan de Geus, Joop van der Vaart: Happy Cubes (Wirrel
Warrel), Cubism For Fun (CFF), published by the Nederlandske Kubus Club
(NKS), Part 50/4, (1999)
Happy Cube
on the Internet top
German
Reich der Spiele
Happy
Cube
Wikipedia
Happy
Cube
English
Dirk Laureyssens
The
homepage of the inventor of Happy Cube
Happy Cube
SourceForge
Happy
Cube Solver
Snafooz (The
American copy of Happy Cube), Snafooz
Solutions
Thomer Gil
Happy Cube (Wirrel
Warrel) Solver
Wikipedia
Happy
Cube
Spanish
NN
Evalandia.Soluciones
Cococrash
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |
