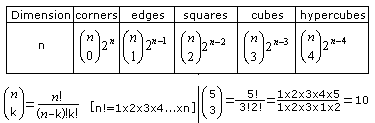|
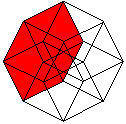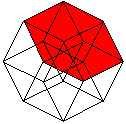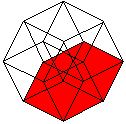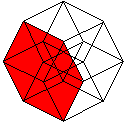
What is the Hypercube?
The hypercube is the cube with four dimensions.
Our imagination is not sufficient enough to understand
the fourth dimension and the hypercube.
You can approach the hypercube through analogy to the
3-dimensional cube from different sides. So you can become familiar with
it.
Cubes in Perspective
top
...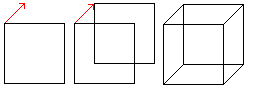 ... ... |
If you move a square parallel in plane and join the corresponding
corners, you get the perspective sight of the cube. |
...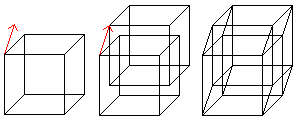 ... ... |
If you move a cube parallel in space and join the corresponding
corners, you get the perspective sight of the hypercube. |
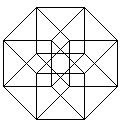
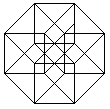
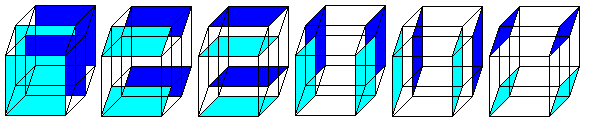
The hypercube has 16 corners (derived from 2 cubes) and 32
edges (2 cubes and joining lines).
... ... ... |
|
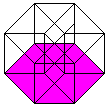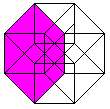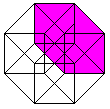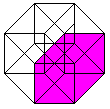
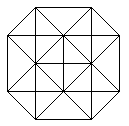
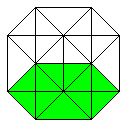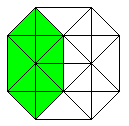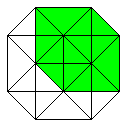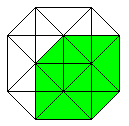
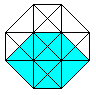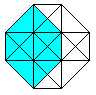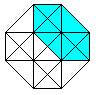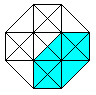
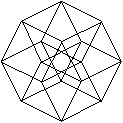
The hypercube has 24 squares.
...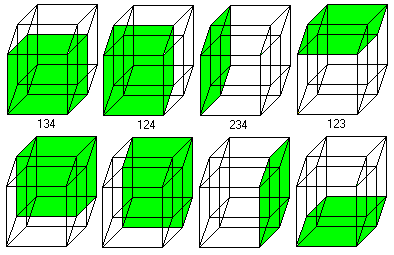 ... ... |
The cube is covered by six squares.
In the same way eight cubes
form the hypercube. |
The numbers 134, 124, 234, 123 indicate the base vectors
(declared below).
If you know the 3D view, you can look at the hypercube
three-dimensionally, too.
Central Projections
top
...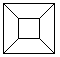 ......... ......... |
The cube is distorted in a central projection. 4 of the
6 squares appear as trapeziums, which lie between the small and the big
square. |
...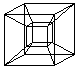 .... .... |
A representation of the hypercube has been developed
of this.
(Viktor Schlegel, 1888) |
...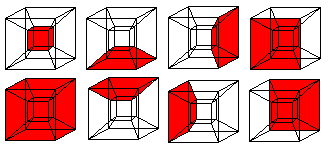 ... ... |
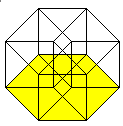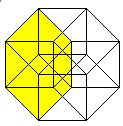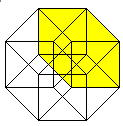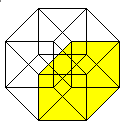
6 of the 8 cubes appear as pyramid stumps,
which lie between the small and the big cube. |
 |
4 cubes, 6 squares, and 4 edges meet at each corner.
3 cubes and 3 squares meet at each edge.
2 cubes meet at each square.
Nets top
...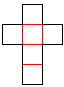 ......... ......... |
If you spread out the cube, you get its net. Together
the six squares have 6x4=24 sides. 2x5=10 sides (red) are bound. If you
build a cube, you have to stick the remaining 14 sides in pairs.
There are 11 nets.
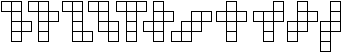
|
...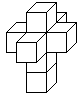 ...... ...... |
If you spread out the hypercube, you get its net as an
arrangement of 8 cubes. Together the eight cubes have 8x6=48 squares. 2x7=14
squares are bound. If you "build" a hypercube, you have to stick the remaining
34 squares in pairs.
How many nets are there?
Peter Turney and Dan Hoey counted 261 cases. |
Cross-Sections top
..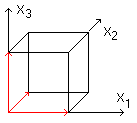 ... ... |
A cube (more exact: a cube with the edges 1) is produced
by three unit vectors (red) perpendicular to each other.
They form a coordinate system. |
... ........ ........
|
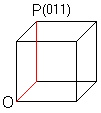
A triplet formed by the numbers 0 or 1 describes the
corners. The triplet (011) belongs to the point P. You reach P by going
from the origin O first in x2 direction and then in x3 direction. This
way is fixed by 011. |
...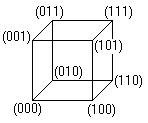 ...... ...... |
You describe all the 8 corners by coordinates in this
manner. All combinations of three numbers using 0 or 1 occur as coordinates. |
...... ......... .........
|
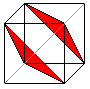
If you add the coordinates of one point, you get the
sums 0,1,2, or 3. The sums 0 and 3 belong to opposite corners. They are
ending points of a diagonal (green). If you join the points with the sums
1 or 2, you get triangles (red). |
If you write x1+x2+x3=a and substitute all numbers between
0 and 3 with a, you find to every value another plane. The hexagon corresponding
to a=1.5 is famous.
top
...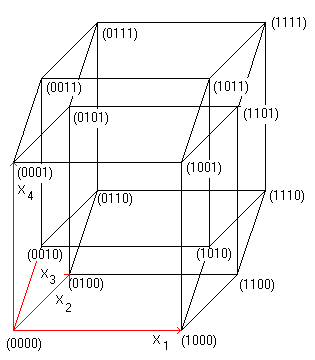 ... ... |
Corresponding to the cube four basic vectors (red) produce
the hypercube.
All combinations of four numbers using 0 or 1 occur as
coordinates. |
...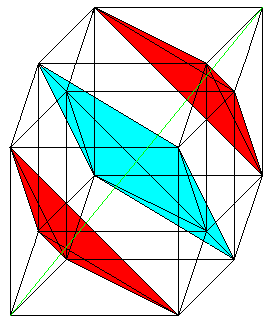 ...... ...... |
If you add the coordinates of one point, you get the
sums 0,1,2,3, or 4. The sums 0 and 4 belong to opposite corners. They are
ending points of a diagonal (green). If you join the points with the sums
1 or 3, you get two tetrahedra (red).
If you join the points with the sum 2, you get an octohedron
(blue).
If you write x1+x2+x3+x4=a and substitute all numbers
between 0 and 4 with a, you find another body as a section to every value.
The section is perpendicular to the diagonal from (0000)
to (1111).
|
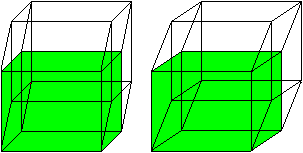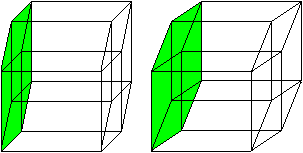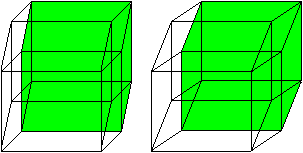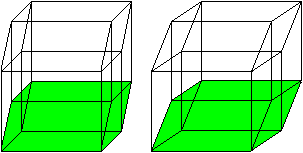
More Drawings top
The n-dimensional
Cube top
The hypercube is a construct of ideas. You receive a
plausible explanation for its features by the "permanent principle", which
often is used in mathematics to get from the "known to the unknown".
Cubes with the dimensions 1, 2 and 3 have the properties
as follows.
The data of the hypercube might follow in the next line.
Dimension=4 and corners=16 are clear.
There are formulas for continuing the sequence for the
edges and squares.
If you take n=4, you get the data of the hypercube.
Encore: Data of the 5-dimensional cube
The Hypercube
on the Internet top
English
Eric W. Weisstein, (MathWorld)
Hypercube
Peter Turney
Unfolding
the Tesseract
Wikipedia
Hypercube,
Tesseract,
Fourth
dimension, Joseph
Cross (tower)
German
Frank Richter
living
in the hyperspace
Hans Walser
Der
n-dimensionale Hyperwürfel (.pdf-Datei)
Manfred Hörsch
Hyperkubus
- Videos
Roberto Neumann
Hyperwürfel
und Hyperkugeln
Wikipedia
Hyperwürfel,
Tesserakt,
4D,
Josephskreuz
References top
(1) Martin Gardner: Mathematischer Karneval, Frankfurt
am Main, 1975
(2) R.Thiele, K.Haase: Der verzauberte Raum, Leipzig,
1991
Feedback: Email address
on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |
 ...
... ...
... ...
... ...
...
 .........
......... ....
.... ...
...
 .........
.........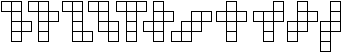
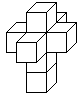 ......
...... ...
... ........
........ ......
...... .........
......... ...
... ......
......