|
What is the Snake Cube?
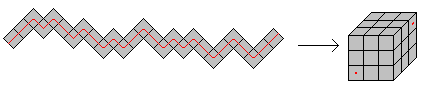The snake cube is a chain of 27 cubes. The cubes are connected
by an elastic band running through the middle. There are 17 groups with
two or three cubes shown in the drawing.
The aim of the puzzle is to arrange the chain in such
a way that there will be a 3x3x3 cube.
Ways to the Solution
top
You can only solve the snake cube systematically.
 |
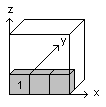First you number the pairs or triplets of cubes from
1 to 17.
You see triplet number 1 on the left. While ordering
you should always keep the same orientation in the room.
You fix this orientation by a coordinate system with
x-, y- and z-axis. |
You learn from a diagram how to arrange the 16 following
groups. There are also dead ends with STOP to show the structure
of this puzzle. I will explain the names of the moves by an example. "10-x"
means: Arrange the 10th group in direction of
the -x-axis.
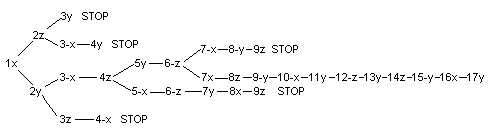If you see the simple diagram you may wonder why this puzzle
is so difficult. The reason is that you often have to go back to the last
branch. It is difficult to find this place.
There is another solution. You start at the end, but then
you will have technical problems. The middle vertical triplet is late and
can be laid properly only with difficulties.
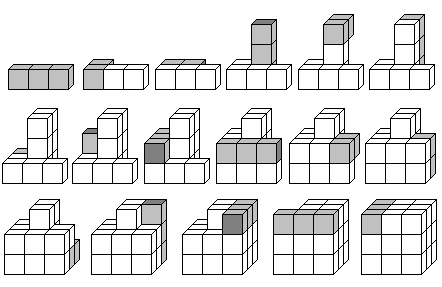
There are two more solutions because of symmetry. You
can see one of these in a sequence of drawings.
The Solution
in 17 Steps top
|
........ ........
|
Twelve Cubes top
I 've got this nice cube chain. I don't know the name
and the manufacturer. Obviously it is similar to the "Kibble Cube".
... ... |
The shape is simple:
There are two slits turned around 90° in opposite
faces of one cube. The 12 cubes are connected by an elastic string
along the centre axes. The first and the last cube have a knot inside. |
You can give the cube chain any direction in this arrangement.
Chain of 20
cubes
There is a competition for pupils
of Primary Schools in Germany called Känguru-Wettbewerb.
A chain of 20 cubes was the prize in 2017.
|
Paul built the cube body of 20 cubes. |
Chain
of 27 cubes
If you would have 27 cubes instead of 12 or 20, you could
lay the snake cube above.
Snake
Cube on the Internet top
English
Jaap Scherphuis
Snake
Cube , Kibble
Cube
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |
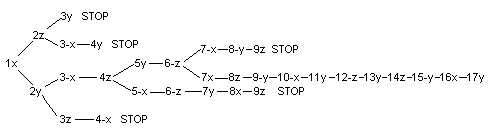
