|
What is a spiral?
A spiral is a curve in the plane or in the space, which runs around
a centre in a special way.
Different spirals follow. Most of them
are produced by formulas.
Spirals by Polar Equations
top
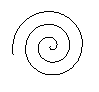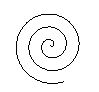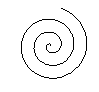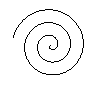
Archimedean Spiral top
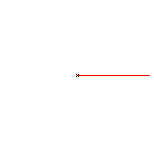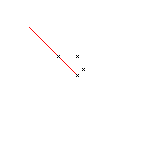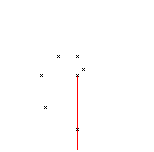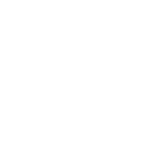
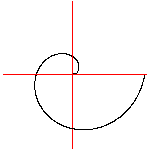
You can make a spiral by two motions of a point: There is a uniform
motion in a fixed direction and a motion in a circle with constant speed.
Both motions start at the same point.
.......................... . |
|
|
(1) The uniform motion on the left moves a point to the right. - There
are nine snapshots.
(2) The motion with a constant angular velocity moves the point on
a spiral at the same time. - There is a point every 8th turn.
(3) A spiral as a curve comes, if you draw the point at every turn.
You get formulas analogic to the circle
equations.
Circle
 |
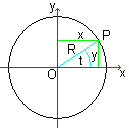Let P be a point of a circle with the radius R, which is given by an
equation in the centre position.
There are three essential descriptions of the circle:
(1) Central equation: x²+y² = R² or [y = sqr(R²-x²)
und y = -sqr(R²-x²)],
(2) Parameter form: x(t) = R cos(t), y(t) = R sin(t),
(3) Polar equation: r(t) = R. |
You give a point by a pair (radius OP, angle t) in the (simple) polar equation.
The radius is the distance of the point from the origin (0|0). The angle
lies between the radius and the positive x-axis, its vertex in the origin.
Spiral
The radius r(t) and the angle t are proportional for the simpliest
spiral, the spiral of Archimedes. Therefore the equation is:
(3) Polar equation: r(t) = at [a is constant].
From this follows
(2) Parameter form: x(t) = at cos(t), y(t) = at sin(t),
(1) Central equation: x²+y² = a²[arc tan (y/x)]².
... ...
|
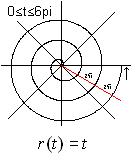The Archimedean spiral starts in the origin and makes a curve with
three rounds.
The distances between the spiral branches are the same.
More exact: The distances of intersection points along a line through
the origin are the same. |
... ... |
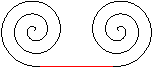If you reflect an Archimedean spiral on a straight line, you get a
new spiral with the opposite direction.
Both spirals go outwards. If you look at the spirals, the left one
forms a curve going to the left, the right one forms a curve going to the
right. |
If you connect both spirals by a straight (red) or a bowed curve, a double
spiral develops.
Equiangular Spiral (Logarithmic
Spiral, Bernoulli's Spiral) top
... ...
|
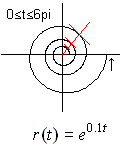(1) Polar equation:
r(t) = exp(t).
(2) Parameter form: x(t) = exp(t) cos(t),
y(t) = exp(t) sin(t).
(3) Central equation:
y = x tan[ln(sqr(x²+y²))].
The logarithmic spiral also goes outwards.
The spiral has a characteristic feature: Each
line starting in the origin (red) cuts the spiral with the same angle. |
More Spirals top
If you replace the term r(t)=at of the Archimedean
spiral by other terms, you get a number of new spirals. There are six spirals,
which you can describe with the functions f(x)=x^a [a=2,1/2,-1/2,-1] and
f(x)=exp(x), f(x)=ln(x). You distinguish two groups depending on how the
parameter t grows from 0.
...... ......... |
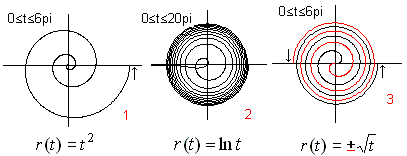If the absolute modulus of a function r(t) is increasing, the spirals
run from inside to outside and go above all limits.
The spiral 1
is called parabolic spiral or Fermat's spiral. |
.. .... |
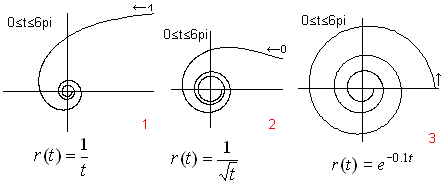If the absolute modulus of a function r(t) is decreasing, the spirals
run from outside to inside. They generally run to the centre, but they
don't reach it. There is a pole.
Spiral 2 is
called the Lituus (crooked staff). |
I chose equations for the different spiral formulas suitable for plotting.
Clothoide (Cornu Spiral) top
.. .... |
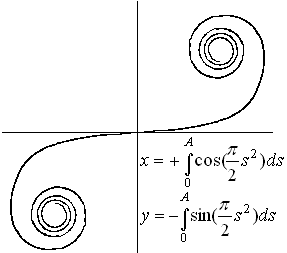The clothoid or double spiral is a curve, whose curvature grows with
the distance from the origin. The radius of curvature is opposite proportional
to its arc measured from the origin.
The parameter form consists of two equations with Fresnel's integrals,
which can only be solved approximately.
You use the Cornu spiral to describe the energy distribution of Fresnel's
diffraction at a single slit in the wave theory. |
Spirals Made of Arcs top
Half circle spirals
 |
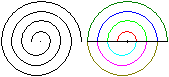You can add half circles growing step by step to get spirals.
The radii have the ratios 1 : 1.5 : 2 : 2.5 :
3..... |
Fibonacci Spiral
... ... |
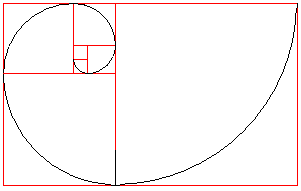Draw two small squares on top of each other. Add a sequence of growing
squares counter clockwise.
Draw quarter circles inside the squares (black).
They form the Fibonacci Spiral. |
The Fibonacci spiral is called after its numbers. If you take the length
of the square sides in the order, you get the sequence 1,1,2,3,5,8,13,21,
... These are the Fibonacci numbers, which you can find by the recursive
formula a(n)=a(n-1)+a(n-2) with [a(1)=1, a(2)=1, n>2].
Spirals Made of Line
Segments top
... ...
|
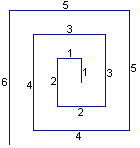The spiral is made by line segments with the lengths 1,1,2,2,3,3,4,4,....
Lines meet one another at right angles. |
... ... |
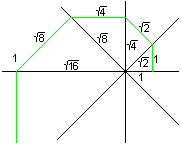Draw a spiral in a crossing with four intersecting straight lines,
which form 45° angles. Start with the horizontal line 1 and bend the
next line perpendicularly to the straight line. The line segments form
a geometric sequence with the common ratio sqr(2).
If you draw a spiral into a straight line bundle, you approach the logarithmic
spiral, if the angles become smaller and smaller. |
... ... |
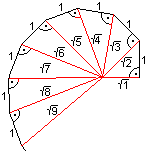The next spiral is formed by a chain of right angled triangles, which
have a common side. The hypotenuse of one triangle becomes the leg of the
next. First link is a 1-1-sqr(2)-triangle.
The free legs form the spiral.
It is special that the triangles touch in line segments. Their lengths
are the roots of the natural numbers. You can proof this with the Pythagorean
theorem.
This figure is called root spiral or root snail or wheel of Theodorus. |
... ... |
Squares are turned around their centre with 10° and compressed
at the same time, so that their corners stay at the sides of their preceding
square.
Result: The corners form four spiral arms. The spiral is similar to
the logarithm spiral, if the angles get smaller and smaller.
You can also turn other regular polygons e.g. an equilateral triangle.
You get similar figures. |
This picture reminds me of the programming language LOGO of the early days
of computing (C64-nostalgia).
Three-dimensional Spirals
top
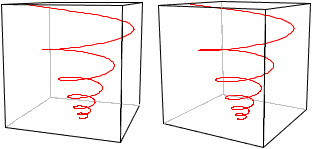
Helix
... ... |
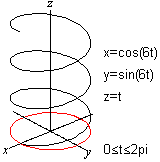If you draw a circle with x=cos(t) and y=sin(t) and pull it evenly
in z-direction, you get a spatial spiral called cylindrical spiral or helix. |
The picture pair makes a 3D view possible.
... ... |
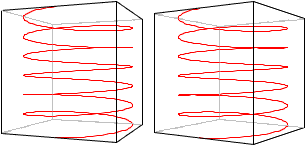
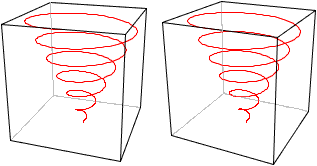
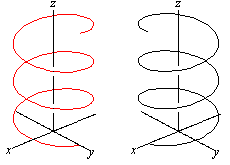Reflect the 3D-spiral on a vertical plane. You get a new spiral (red)
with the opposite direction.
If you hold your right hand around the right spiral and if your thumb
points in direction of the spiral axis, the spiral runs clockwise upward.
It is right circular.
You must use your left hand for the left spiral. It is left circular.
The rotation is counter clockwise.
Example: Nearly all screws have a clockwise rotation, because most of
the people are right-handed. |
... ... |
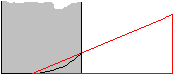In the "technical" literature the right circular spiral is explained
as follows: You wind a right- angled triangle around a cylinder. A clockwise
rotating spiral develops, if the triangle increases to the right. |
Conical Helix
top
You can make the conical helix with the Archimedean spiral or equiangular
spiral.
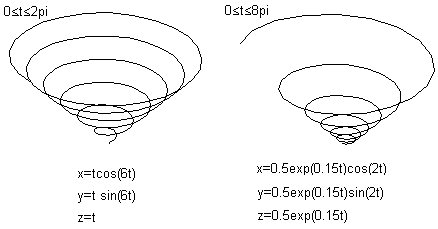
The picture pairs make 3D views possible.
Loxodrome,
Spherical Helix
... ... |
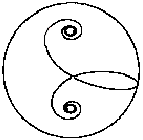The loxodrome is a curve on the sphere, which cuts the meridians at
a constant angle. They appear on the Mercator projection as straight lines.
The parametric representation is
x=cos(t) cos [1/tan (at)]
y=sin(t) cos[1/tan (at)]
z= -sin [1/tan (at)] (a is constant)
You can find out x²+y²+z²=1. This equation means that
the loxodrome is lying on the sphere. |
Generally there is a loxodrome at every solid made by rotation about an
axis.
Making of Spirals top
 |
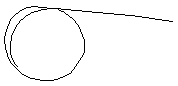A strip of paper becomes a spiral, if you pull the strip between the
thumb and the edge of a knife, pressing hard. The spiral becomes a curl
where gravity is present. |
You use this effect to decorate the ends of synthetic materials, such as
the narrow colourful strips or ribbons used in gift-wrapping.
I suppose that you have to explain this effect in the same way as a
bimetallic bar. You create a bimetallic bar by glueing together two strips,
each made of a different metal. Once this bimetallic bar is heated, one
metal strip expands more than the other causing the bar to bend.
The reason that the strip of paper bends is not so much to do with
the difference in temperature between the top and bottom side. The knife
changes the structure of the surface of the paper. This side becomes 'shorter'.
Incidentally, a strip of paper will bend slightly if you hold it in
the heat of a candle flame.
... ... |
Forming curls reminds me of an old children's game: Take a dandelion
flower and cut the stem into two or four strips, keeping the head intact.
If you place the flower into some water, so that the head floats on the
surface, the strips of the stem will curl up. (Mind the spots.)
A possible explanation: Perhaps the different absorption of water on
each side of the strips causes them to curl up. |
Mandelbrot Set Spirals top
The coordinates belong to the centre of the pictures.
You also find nice spirals as Julia Sets. Here is an example:
You find more about these graphics on my page Mandelbrot
Set.
Spirals Made of Metal top
You find nice spirals as a decoration of barred windows, fences, gates
or doors. You can see them everywhere, if you are look around.
... ... |
I found spirals worth to show at New Ulm, Minnesota, USA.
Americans with German ancestry built a copy of the Herman monument near
Detmold/Germany in about 1900.
Iron railings with many spirals decorate the stairs (photo).
More about the American and German Herman on Wikipedia-pages (URL below) |
Costume jewelleries also take spirals as
motive.
... ...
|
Annette's spiral
 |
Spirals, Spirals, Spirals
top
Ammonites, antlers of wild sheep, Archimedes' water spiral, area of
high or low pressure, arrangement of the sunflower cores, @, bimetal thermometer,
bishop staff, Brittany sign, circles of a sea-eagle, climbs, clockwise
rotating lactic acid, clouds of smoke, coil, coil spring, corkscrew, creepers
(plants), curl, depression in meteorology, disc of Festós, double
filament of the bulb, double helix of the DNA, double spiral, electron
rays in the magnetic longitudinal field, electrons in cyclotron, Exner
spiral, finger mark, fir cone, glider ascending, groove of a record,
head of the music instrument violin, heating wire inside a hotplate, heat
spiral, herb spiral, inflation spiral, intestine of a tadpole, knowledge
spiral, licorice snail, life spiral, Lorenz attractor, minaret at Samarra
(Iraq), music instrument horn, pendulum body of the Galilei pendulum, relief
strip of the Trajan's column at Rome or the Bernward column at Hildesheim,
poppy snail, road of a cone mountain, role (wire, thread, cable, hose,
tape measure, paper, bandage), screw threads, simple pendulum with friction,
snake in resting position, snake of Aesculapius, snail of the interior
ear, scrolls, screw alga, snail-shell, spider net, spiral exercise book,
spiral nebula, spiral staircase (e.g. the two spiral stairs in the glass
dome of the Reichstag in Berlin), Spirallala ;-), Spirelli noodles,
Spirills (e.g. Cholera bacillus), springs of a mattress, suction trunk
(lower jaw) of the cabbage white butterfly, tail of the sea-horse, taps
of conifers, tongue and tail of the chamaeleon, traces on CD or DVD, treble
clef, tusks of giants, viruses, volute, watch spring and balance spring
of mechanical clocks, whirlpool, whirlwind.
Spirals on the Internet top
German
Asti
BEWEGUNGSFUNKTIONEN
Spiralen
D.H.O. Braasch
Spiralen
als Symbol der Sonnenbahn
Jürgen Berkemeier
Spiralen
Matheprisma
Bewegungsfunktionen
(Spiralen 1 ) - (Spiralen online zeichnen)
Michael Komma
Fresnel-Beugung
am Einzelspalt (Cornu-Spirale)
Susanne Helbig, Kareen Henkel und Jan Kriener
Spiralen
in Naturwissenschaft, Technik und Kunst
Stephan Jaeckel und Sergej Amboni
Spiralen
in Natur, Technik und Kunst
(Referenz: Heitzer J, Spiralen, ein Kapitel phänomenaler Mathematik,
Leipzig 1998)
Wikipedia
Spirale, Klothoide,
Logarithmische
Spirale, Fibonacci
Folge, Loxodrome,
Ulam-Spirale
Hermannsdenkmal,
Hermann
Heights Monument
English
A Pocket Art Show Production in association with the Pataphysics Department
at the Quantum Mechanics Institute, Keighley
Fraktal
Ayhan Kursat ERBAS
Equiangular
Spiral
Bob Allanson
This is a
logarithmic spiral
David Eppstein (Geometry Junkyard)
Spirals
Eric W. Weisstein (MathWorld)
Spirals:
Archimedean
Spiral, Circle
Involute, Conical
Spiral, Cornu
Spiral, Curlicue
Fractal, Fermat's
Spiral, Helix,
Hyperbolic
Spiral, Logarithmic
Spiral, Mice
Problem, Nielsen's
Spiral, Polygonal
Spiral, Prime
Spiral, Rational
Spiral, Seashell,
Spherical
Spiral
Hop David (Hop's Gallery)
Riemann sphere,
Ram's
Horn,
Spiral
Tile
Ivars Peterson
Pursuing
Pursuit Curves
Jan Wassenaar
spiral
Jim Bumgardner
A musical realization
of the motion graphics of John Whitney as described in his book "digital
harmony"
John Macnab
Sculptures
Keith Devlin
The Double Helix
Mark Newbold
Counter-Rotating
Spirals Illusion
Richard Parris (peanut Software)
Program WINPLOT
Xah Lee
Equiangular
Spiral, Archimedean
Spiral, Lituus,
Cornu
Spiral
Wikipedia
Spiral, Archimedean
spiral, Cornu
spiral, Fermat's
spiral, Hyperbolic
spiral, Lituus,
Logarithmic
spiral,
Fibonacci spiral,
Golden
spiral,
Rhumb line,
Ulam
spiral
Hermann
Heights Monument,
Hermannsdenkmal
French
Robert FERRÉOL (COURBES
2D )
SPIRALE
COURBES
3D (SPHÉRO-CYLINDRIQUE, SPIRALE CONIQUE DE PAPPUS, SPIRALE CONIQUE
DE PIRONDINI, SPIRALE SPHÉRIQUE)
You can read this page in Haitian
Creole translation.
References top
(1) Martin Gardener: Unsere gespiegelte Welt, Ullstein, Berlin, 1982
[ISBN 3-550-07709-2]
(2) Rainer und Patrick Gaitzsch: Computer-Lösungen für Schule
und Studium, Band 2, Landsberg am Lech, 1985
(3) Jan Gullberg: Mathematics - From the Birth of Numbers, New York
/ London (1997) [ISBN 0-393-04002-X]
(4) Khristo N. Boyadzhiev: Spirals and Conchospirals in the Flight
of Insects, The College Mathematics Journal, Vol.30, No.1 (Jan.,1999) pp.23-31
(5) Jill Purce: the mystic spiral - Journey of the Soul, Thames and
Hudson, 1972, reprinted 1992
Feedback: Email address on my main page
This
page is also available in German
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
Jürgen Köller 2002
top |
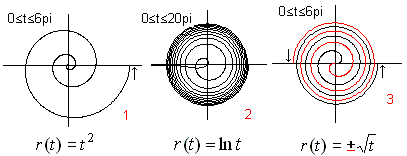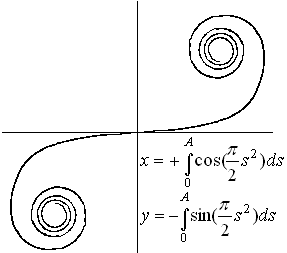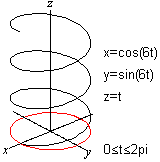
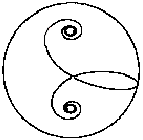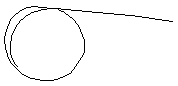