What is a Tetrahedron?
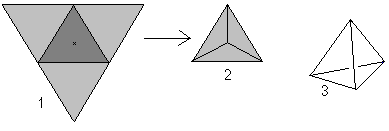 A tetrahedron is a three-dimensional figure with four equilateral
triangles. If you lift up three triangles (1), you get the tetrahedron
in top view (2). Generally it is shown in perspective (3).
A tetrahedron is a three-dimensional figure with four equilateral
triangles. If you lift up three triangles (1), you get the tetrahedron
in top view (2). Generally it is shown in perspective (3).
If you look at the word tetrahedron (tetrahedron means
"with four planes"), you could call every pyramid with a triangle as the
base a tetrahedron.
However the tetrahedron is the straight, regular triangle
pyramid on this website.
Pieces of the
Tetrahedron
top
Height and area of a lateral triangle
Four equilateral triangles form a tetrahedron.
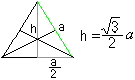 ... ... |
A triangle is picked out: The three heights intersect
each other in one point as in every triangle. This is the centre of the
triangle. The height can be calculated by the side a as h=sqr(3)/2*a using
the Pythagorean theorem. |
The heights also are medians and intersect with the ratio
2:1. That is used in the following calculations.
The area of the triangle is A=sqr(3)/4*a².
Space Height
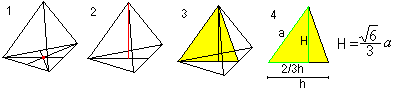 The height of the tetrahedron is between the centre of the
basic triangle (1) and the vertex (2). For calculations you regard the
so-called support triangle (3, yellow), which is formed by
one edge and two triangle heights. There is H=sqr(6)/3*a using the Pythagorean
theorem.
The height of the tetrahedron is between the centre of the
basic triangle (1) and the vertex (2). For calculations you regard the
so-called support triangle (3, yellow), which is formed by
one edge and two triangle heights. There is H=sqr(6)/3*a using the Pythagorean
theorem.
Centre, Circumscribed
Sphere, and Inscribed Sphere
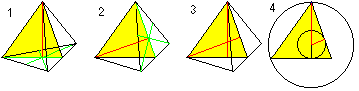 The centre of a tetrahedron is the intersection of two space
heights (1,2,3). It is centre of gravity, centre of the sphere through
the four corners, and centre of the largest sphere, which still fits inside
the tetrahedron (4).
The centre of a tetrahedron is the intersection of two space
heights (1,2,3). It is centre of gravity, centre of the sphere through
the four corners, and centre of the largest sphere, which still fits inside
the tetrahedron (4).
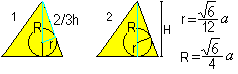 ... ... |
You get two formulas for r and R with the help of the
Pythagorean theorem (1) and H=R+r (2):
There is r=sqr(6)/12*a , R=sqr(6)/4*a. |
Angle
...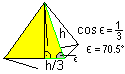 ... ... |
The angle of inclination (edge angle) between a lateral
triangle and the base is seen in the yellow support triangle.
There is 70,5°. |
Surface
....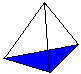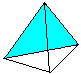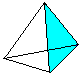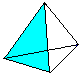 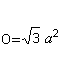 ..... ..... |
The area of the base and the lateral faces form the surface
O. There is O=4*A (triangle) = sqr(3)a². |
Volume

If you put a prism (1) with the volume A(triangle)*H around
the tetrahedron and move the vertex to the corners of the prism three times
(2,3,4), you get three crooked triangle pyramids with the same volume.
They fill the prism (5).
Thus the volume of a triangle pyramid is (1/3)*A(triangle)*H.
There is V=sqr(2)/12*a³ for the tetrahedron.
Tetrahedal Numbers
top
...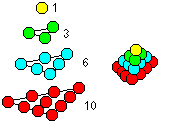 ... ... |
You can build a tetrahedron with layers of spheres. The
number of the spheres in one layer is 1,3,6,10..., generally n(n+1)/2.
If you add the spheres layer by layer, you get the tetrahedral
numbers 1,4,10,20,..., generally 1+3+6+10+...+n(n+1)/2=n(n+1)(n+2)/6. |
...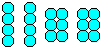 ... ... |
If you glue 20 marbles to two groups with four and two
with six, you get a well known puzzle: You must form a pyramid with four
pieces. |
There are many similar puzzles.
Tetrahedron in
the Cube top
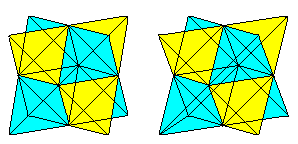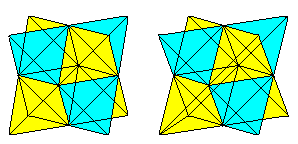
Six face diagonals form a tetrahedron in the cube.
If you know the 3D-view, you can three-dimensionally
look at the following two cube pairs.
 The volume of the tetrahedron is the third part of the volume
of the cube.
The volume of the tetrahedron is the third part of the volume
of the cube.
If you draw a second tetrahedron and the lines of intersection,
you get a penetration of two tetrahedrons.
The figure consists of the face diagonals and the connecting
lines of the centres of the lateral squares of the original cube. The last
ones form an octahedron.
Rings of Tetrahedrons
top
You can make paper tetrahedrons and stick an even number
of them to a ring. The ring can continually twist inwards or outwards through
the centre. This is a pretty toy. - These rings are also called kaleidocycles.
You find more on my web page Kaleidocycles.
Tetrahedra
on the Internet top
German
Christof Weber
Was
hat dieser Körper mit Kugeln zu tun? (Reuleaux'sche
Tetraeder)
FAZ
Tetraederpackung:
Eins geht noch
Georg Burkhard
Pyramide
des Cestius, Rom (u.a.)
Gerd Müller
Platonische
Körper in Stereodarstellung
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetraeder
LANDRAT-LUCAS-GYMNASIUM Leverkusen
Sierpinski
Tetraeder
Wikipedia
Tetraeder,
Tetraeder
(Bottrop),
Tetrapode,
Tetraederzahl
English
Eric W. Weisstein (World of Mathematics)
Tetrahedron
H.B.Meyer (Polyeder aus Flechtstreifen)
Tetrahedron
Wikipedia
Tetrahedron,
Tetrapod
(structure), Tetrahedral
number
Gail from Oregon, thank you for supporting me in
my translation.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |

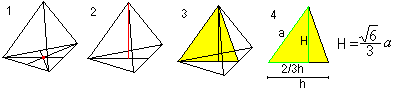
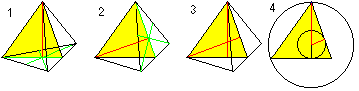



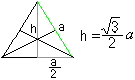 ...
... ...
...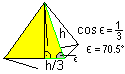 ...
...
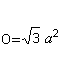 .....
..... ...
...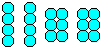 ...
...