What is a Square Number?
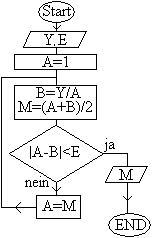
On the other hand a square number results by multiplying an integer by itself. Formula: a*a=a²=k (a and k stand for integers.) The same factor is called the base. After this a fractal number like the 4/9=(2/3)² is suspended. These are the first 100 square numbers. 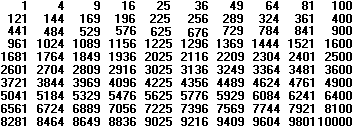 You can illustrate square numbers by the following drawings.
You can see: Only the digits 0, 1, 4, 5, 6 or 9 are on the ones place. Thoughts concerning this point: Consider numbers with three digits. They can be written as 100c+10b+a. The letters a, b, and c stand for digits. There is (100c+10b+a)² = [(100c+10b)+a]² = (100c+10b)²+2(100c+10b)a+a² = 100(10c+b)²+10(20c+2b)a+a² = 10{[10(10c+b)²]+(20c+2b)a}+a². That means that the square of a three-digit number has the form 10x+a². Therefore the digit on the ones place is given only by a², and these are 0, 1, 4, 9 or the last digits of 16, 25, 36, 49, 64 und 81. These principles can be transferred to all multi-digit
numbers.
Square Root top
132²=17424 leads to the square root sqrt(17424)=132.
Today there is no problem to find square roots. There
are calculators.
More methods follow shown by the example. 1 Determination by nested intervals sqrt(17424) The number must be between 100 and 200 (100²=10000 and 200²=40000). It must be between 130 and 140 (130²=16900 and 140²=19600). The 4 of 17424 is in the ones place. Then 132 and 138 come into consideration. Result: sqrt(17424)=132 2 Determination by factorization sqrt(17424) You write the number in factors and develop the square number this way. 17424 = 8*2178 = 16*1089 = 16*9*121. Thus the root is 4*3*11=132. Result: sqrt(17424)=132 3 School method from former times This is a kind of long division. 1
2
3
4
5
6
7
The explanation of this method results from the "trinomic formula" (a+b+c)²=a²+b²+c²+2ab+2ac+2bc.
Before the age of calculators this method was standard in German schools and was practised a lot. Today this is history. (5, page 47 "Wurzelziehen per Hand") 4 Computing the square root of a positive number by Newton's method The square root of 17.424 will be found by the convergent sequence x1=1 and xk=(xk-1+n/xk-1)/2 for k>1. Maybe it is interesting for younger people to see how this method was programmed and illustrated in former times. The common programming language was BASIC in the 1970s.
It is surprising that the square root 132 is not found earlier than after ten steps. The reason is the bad start number A=1. It is better, if near the root. The Heron ansatz is A=Y. Sequences top
It is better to look at sets. The sets of the natural and square numbers are equivalent. There is no doubt that there are more natural numbers than square numbers up to a certain number. This statement is on the view of set theory: The set of the square numbers is a subset of the natural numbers. To the second sequence The sequence of the square numbers is also an arithmetic series of second order. A figure follows to explain this. The second line is the sequence of the odd numbers. The feature is that you reach a constant difference 2 after two steps. Hence the sequence of square numbers has constant differences of differences. To the third sequence s1=1²=1 s2=1²+2²=5 s3=1²+2²+3²=14 s4=1²+2²+3²+4²=30, ... Generally it is sn=1²+2²+3²+...+n²=n(n+1)(2n+1)/6 . Here is a proof, which is unusual.
(4, page 28f.) To the 4th and 5th sequences The 4th sequence is 1/1, 1/4, 1/9, 1/16, ... , 1/n². It has the limit 0 for n over all limits. The associated series 1/1+1/4+1/9+1/16+ ... +1/n²is interesting. It is convergent and has the limit pi²/6 (Euler) or rounded 1.65. (3, page 93f. and page 241) The series of prime numbers developed by the prime numbers (the sum of 1/p) is divergent. Hence you can imply that there are more prime numbers than square numbers for n over all limits (2, page 322). Sums top
Difference of two square numbers Each prime number p>2 can be written as the difference of two square numbers. Example: 37=361-324=19²-18² Division by 8 If you divide the square number of an odd number by 8, you get the remainder 1. Example: 19² : 8 =361 : 8=45+1/8 Lagrange's four-square theorem Each natural number can be written as the sum of four square numbers at least. Example: 85=64+16+4+1 Fermat's two-square theorem A prime number with p=4n+1 can be written as the sum of two square numbers. Examples: 5=1²+2², 13=2²+3², 625=7²+24²=15²+20² Pythagorean triple There are triples of three integers, which follow the formula a²+b²=c². You can read more on my German page 3-4-5-Dreieck. Playing with numbers
top
Calculation of 51² to 59² Example: 56²=3136 (50+E)²=(25+E)100+E² In words: Add 25 to the ones digit and attach the square of the ones digit. Calculation of three-digit numbers with 0 on the tens place. Example: 203²=041209, 609²=370881 (H0E)²=H²*10000+2HE*100+E² In words: The square numbers of the hundreds digit and the square numbers of the ones digit are external. The double product of the hundreds digit and the ones digit are in the centre. If the double product is three-digit, you must add 1 to the square of the hundred digit. Cube numbers are written in the digits 0 to 9. No digit is used twice or more. There are 77 numbers in Lietzmann's book. 1026 753 849=32043² is the smallest number. 9814072356=99066² is the largest number. The ten-digit numbers with different digits are called "pandigital numbers". Cube numbers are written in the digits 1 to 9. No digit is used twice or more. Two examples: 139845276=11826² und 923187456=30384² The nine-digit numbers with different digits are called "zeroless pandigital numbers". Mirror numbers
Consecutive numbers
Palindromes among the square numbers
Five sequences of square numbers
Kaprekar numbers A number like 703 is called Kaprekar number, because it has the following curious feature. If you square the number (703²=494209) and separate the square in 494 and 209, the sum 494+209 is 703 again. The numbers 1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, 7272, 7777 and 9999 are the Kaprekar numbers <10.000. Figurate Numbers
top
You find at MathWorld:
Square Numbers on the Internet top German Andreas Göbel
Matheprisma
Tino Hempel
Wikipedia
English Eric W. Weisstein (MathWorld)
Patrick De Geest (World of Numbers)
Neil J. A. Sloane
Wikipedia
References top
This page is also available in German. URL of
my Homepage:
© 2009 Jürgen Köller |
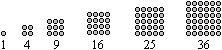
 ...
...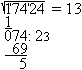 ...
...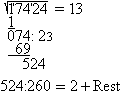 ...
...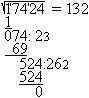 ...
...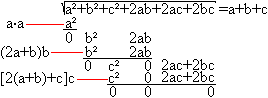 ...
...